设α:x≤-5.β:2m-3≤x≤2m+1.若α是β的必要条件.则实数m的取值范围是(-∞.-3]．题目和参考答案——青夏教育精英家教网——

题目内容

12．设α：x≤-5，β：2m-3≤x≤2m+1，若α是β的必要条件，则实数m的取值范围是（-∞，-3]．

分析根据必要条件的定义建立不等式关系进行求解即可．

解答解：∵α是β的必要条件，
∴β⇒α，
则2m+1≤-5，
即2m≤-6，
得m≤-3，
故答案为：（-∞，-3]

点评本题主要考查充分条件和必要条件的应用，根据充分条件和必要条件的定义建立不等式关系是解决本题的关键．

练习册系列答案

少年素质教育报暑假作业系列答案

金太阳全A加系列答案

创新导学案新课标寒假假期自主学习训练系列答案

超能学典暑假接力棒江苏凤凰少年儿童出版社系列答案

暑假提高班系列答案

完美假期暑假作业系列答案

快乐假期高考状元假期学习方案暑假系列答案

豫欣图书自主课堂系列答案

假期伙伴寒假大连理工大学出版社系列答案

鑫宇文化新课标快乐假期暑假系列答案

相关题目

2．已知函数$f（x）=\left\{{\begin{array}{l}{{x^2}，（x≤0）}\\{\sqrt{4-{x^2}}（x＞0）}\end{array}}\right.$，则$\int_{-1}^2{f（x）dx}$=（　　）

$π-\frac{1}{3}$

$π+\frac{1}{3}$

$\frac{π}{4}+\frac{1}{3}$

$\frac{π}{2}-\frac{1}{3}$

3．已知函数（1）f（x）=3lnx；（2）f（x）=3x²+1；（3）f（x）=3e^x；（4）$f（x）=\frac{3}{x}$．其中满足对于任意x₁∈D（其中D为函数的定义域），相应地存在唯一的x₂∈D，使$\sqrt{f（{x_1}）f（{x_2}）}=3$的函数的序号为（3）、（4）．

20．已知集合$A=\left.{\left\{{x\left|{\frac{3x-5}{x+1}≤1，x∈R}\right.}\right.}\right\}$，集合B={x|x-a|≤1，x∈R}．
（1）求集合A；
（2）若B∩∁_RA=B，求实数a的取值范围．

7．已知集合U={-2，-1，0，1，2}，A={1，2}，B={-2，-1，2}，则A∪（∁_UB）={0，1，2}．

17．一元二次不等式x²+bx+c＜0的解集为{x|1＜x＜2}，则b+c=-1．

4．设集合A={x|1＜x＜3，x∈R}，B={x||x-a|＜4，x∈R}，若x∈A是x∈B的充分条件，求实数a的取值范围．

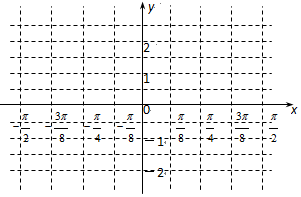已知函数$f（x）=2cosxsin（{x+\frac{π}{3}}）-\sqrt{3}{sin^2}x+sinxcosx$．
（1）求函数f（x）的最小正周期T；
（2）在给出的直角坐标系中，画出函数f（x）在$[{-\frac{π}{2}，\frac{π}{2}}]$上的图象；
（3）若当$x∈[{\frac{π}{12}，\frac{7π}{12}}]$时，f（x）的反函数为f^-1（x），求f^-1（1）的值．

2．椭圆3x²+4y²=6的离心率为（　　）