题目内容
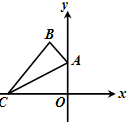 △ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0)
△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0)(1)求AC边上的中线所在直线的方程;
(2)求AC边的垂直平分线的方程.
分析:(1)先求得AC中点D的坐标和直线BD斜率k的值,再用点斜式求得中线BD所在直线的方程.
(2)先求得直线AC斜率,可得AC边的垂直平分线的斜率,再求得AC的中点的坐标,用点斜式求得AC边的垂直平分线的方程.
(2)先求得直线AC斜率,可得AC边的垂直平分线的斜率,再求得AC的中点的坐标,用点斜式求得AC边的垂直平分线的方程.
解答:解:(1)由题意可得,AC中点D(-4,2),且直线BD斜率k=
-2,
故中线BD所在直线的方程:y-2=2(x+4),即2x-y+10=0.
(2)先求得直线AC斜率kAC=
,故AC边的垂直平分线的斜率为k'=-2.
再求得AC的中点为(-4,2),故AC边的垂直平分线的方程y-2=-2(x+4),
即2x+y+6=0.
| 6-2 |
| -2-(-4) |
故中线BD所在直线的方程:y-2=2(x+4),即2x-y+10=0.
(2)先求得直线AC斜率kAC=
| 1 |
| 2 |
再求得AC的中点为(-4,2),故AC边的垂直平分线的方程y-2=-2(x+4),
即2x+y+6=0.
点评:本题主要考查直线的斜率公式、用点斜式求直线的方程,属于基础题.

练习册系列答案
相关题目
已知△ABC的三个顶点分别是A(1,
),B(4,-2),C(1,y),重心G(x,-1),则x、y的值分别是( )
| 3 |
| 2 |
| A、x=2,y=5 | ||
B、x=1,y=-
| ||
| C、x=1,y=-1 | ||
D、x=2,y=-
|
 ,
, ,
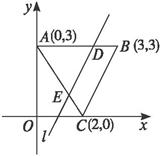
, ,则AC边上的高BD长为( )
,则AC边上的高BD长为( )  B.4 C.5 D.
B.4 C.5 D.