题目内容
如图,已知△ABC的三个顶点分别是A(0,3)、B(3,3)、C(2,0),直线l与BC边平行,分别交AB边、AC边于点D、E,且将△ABC分成面积相等的两部分,求直线l的方程.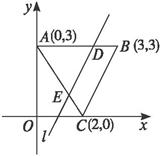
思路解析：利用直线l与BC边平行的条件求出l的斜率,结合定比分点坐标公式求出D点坐标,再由点斜式即可求.
解：∵DE∥BC,∴△ABC∽△ADE.
∴
=
=
=
.
∴点D分
所成比λ=
=
=
+1.
∴xD=
=
,yD=3.∴D(
,3).
又∵kBC=
=3,∴kDE=kBC=3.
∴直线l的方程为y-3=3(x-
),即6x-2y+6-9
=0.
深化升华
“面积比等于相似比的平方”这一结论不仅适用于三角形,对于其他封闭的相似图形也同样适用.本题利用一重要结论,将原问题转化为定比分点问题求解.
练习册系列答案
阅读快车系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使
如图，已知△ABC的顶点坐标依次为A（1，0），B（5，8），C（7，-4），在边AB上有一点P，其横坐标为4，在AC上求一点Q，使线段PQ把△ABC分成面积相等的两部分．
如图，已知△ABC的顶点为A（2，4），B（0，-2），C（-2，3），求：
如图，已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D，以CD为直径的圆分别交BC，CA于点P、Q，求证：线段PQ平分△ABC的周长．
是边长为2的正三角形，则原△ABC的面积为__________.