题目内容
5.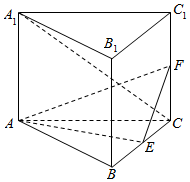 如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.
如图所示,正三棱柱ABC-A1B1C1中,E,F分别是BC,CC1的中点.(Ⅰ)证明:平面AEF⊥平面B1BCC1;
(Ⅱ)若该三棱柱所有的棱长均为2,求三棱锥B1-AEF的体积.
分析 (I)由BB1⊥平面ABC可知BB1⊥AE,又AE⊥BC可得AE⊥平面BCC1B1,从而平面AEF⊥平面B1BCC1;
(II)由(1)知AE为棱锥A-B1EF的高.于是V${\;}_{{B}_{1}-AEF}$=V${\;}_{A-{B}_{1}EF}$=$\frac{1}{3}{S}_{△{B}_{1}EF}•AE$.
解答 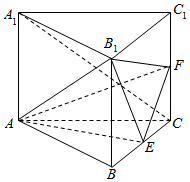 解:(I)∵BB1⊥面ABC,AE?平面ABC,
解:(I)∵BB1⊥面ABC,AE?平面ABC,
∴AE⊥BB1,
∵E是正三角形ABC的边BC的中点,
∴AE⊥BC,
又∵BC?平面B1BCC1,B1B?平面B1BCC1,BC∩BB1=B,
∴AE⊥平面B1BCC1,∵AE?平面AEF,
∴平面AEF⊥平面B1BCC1.
(II)∵三棱柱所有的棱长均为2,
∴AE=$\sqrt{3}$,
∴S${\;}_{△{B}_{1}EF}$=2×2-$\frac{1}{2}×2×1$-$\frac{1}{2}×1×1$$-\frac{1}{2}×2×1$=$\frac{3}{2}$,
由(I)知AE⊥平面B1BCC1
∴${V_{{B_1}-AEF}}={V_{A-{B_1}EF}}=\frac{1}{3}•\frac{3}{2}•\sqrt{3}=\frac{{\sqrt{3}}}{2}$.
点评 本题考查了面面垂直的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
8.停车扬上有3辆小车,2辆摩托车,1辆自行车,为美观环境,要求同类车必须相邻,则不同的停放车辆的方法有( )
| A. | 12种 | B. | 36种 | C. | 48种 | D. | 72种 |
6.与双曲线$\frac{{x}^{2}}{2}$-y2=1有相同的渐近线,且右焦点F到渐近线的距离为2的双曲线方程是( )
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{6}=1$ | B. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{6}=1$ | C. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}=1$ | D. | $\frac{{y}^{2}}{4}-\frac{{x}^{2}}{8}=1$ |
17.给定集合An={1,2,3,…,n},n∈N*.若f是An→An的映射且满足:
①任取i,j∈An,若i≠j,则f(i)≠f(j);
②任取m∈An,若m≥2,则有m∈{f(1),f(2),…,f(m)}.
则称映射f为An→An的一个“优映射”.
例如:用表1表示的映射f:A3→A3是一个“优映射”.
表一
表2
(1)若f:A4→A4是一个“优映射”,请把表2补充完整(只需填出一个满足条件的映射);
(2)若f:A2015→A2015是“优映射”,且f(1004)=1,则f(1000)+f(1017)的最大值为2021.
①任取i,j∈An,若i≠j,则f(i)≠f(j);
②任取m∈An,若m≥2,则有m∈{f(1),f(2),…,f(m)}.
则称映射f为An→An的一个“优映射”.
例如:用表1表示的映射f:A3→A3是一个“优映射”.
表一
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
(2)若f:A2015→A2015是“优映射”,且f(1004)=1,则f(1000)+f(1017)的最大值为2021.
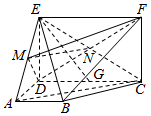 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.
如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.