题目内容
已知f(x)=|2x-
|+|2x+
|.
(1)关于x的不等式f(x)≥a2-a恒成立,求实数a的取值范围;
(2)设m,n∈R+,且m+n=1,求证:
+
≤2
.
| 3 |
| 4 |
| 5 |
| 4 |
(1)关于x的不等式f(x)≥a2-a恒成立,求实数a的取值范围;
(2)设m,n∈R+,且m+n=1,求证:
| 2m+1 |
| 2n+1 |
| f(x) |
考点:绝对值不等式的解法
专题:证明题,不等式的解法及应用
分析:(1)利用绝对值的几何意义可知函数f(x)=|2x-
|+|2x+
|表示数轴上点P(2x)到点A(
)和B(-
)两点的距离,从而可得f(x)min=2,解相应的不等式即可;
(2)利用分析法结合基本不等式即可证得结论.
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
(2)利用分析法结合基本不等式即可证得结论.
解答:
解:(1)依据绝对值的几何意义可知函数f(x)=|2x-
|+|2x+
|表示数轴上点P(2x)到点A(
)和B(-
)两点的距离,
其最小值为f(x)min=2…(3分)
∴不等式f(x)≥a2-a恒成立只需2≥a2-a,解得-1≤a≤2…(5分)
(2)∵f(x)min=2,∴只需证明:
+
≤2
成立,
∵
≤
=m+
;
≤
=n+
.…(8分)
于是
+
≤m+
+n+
=m+n+3=4,
∴
+
≤2
成立,
故要证明的不等式成立.…(10分)
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
其最小值为f(x)min=2…(3分)
∴不等式f(x)≥a2-a恒成立只需2≥a2-a,解得-1≤a≤2…(5分)
(2)∵f(x)min=2,∴只需证明:
| 2m+1 |
| 2n+1 |
| 2 |
∵
| 2(2m+1) |
| 2+(2m+1) |
| 2 |
| 3 |
| 2 |
| 2(2n+1) |
| 2+(2n+1) |
| 2 |
| 3 |
| 2 |
于是
| 2(2m+1) |
| 2(2n+1) |
| 3 |
| 2 |
| 3 |
| 2 |
∴
| 2m+1 |
| 2n+1 |
| 2 |
故要证明的不等式成立.…(10分)
点评:本题考查绝对值不等式的解法,考查绝对值的几何意义与基本不等式的应用,考查分析、运算与论证能力,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
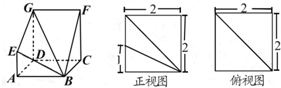 如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图: