题目内容
8．设△ABC的内角A，B，C的对边分别为a，b，c，且$a=2，cosC=-\frac{1}{4}$，3sinA=2sinB（1）求边b和边c；
（2）求△ABC的面积．
分析 （1）由3sinA=2sinB即正弦定理可得3a=2b，由a=2，即可求得b，利用余弦定理结合已知即可得解．
（2）利用同角三角函数基本关系式可求sinC的值，根据三角形面积公式即可得解．
解答 解：（1）△ABC中，∵3sinA=2sinB，
∴由正弦定理可得：3a=2b，
∵a=2，
∴可解得b=3，
又∵cosC=-$\frac{1}{4}$，
∴由余弦定理可得：c2=a2+b2-2abcosC=4+9-2×2×3×（-$\frac{1}{4}$）=16，
∴解得：c=4．
（2）∵cosC=-$\frac{1}{4}$，可得：sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{15}}{4}$，
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×2×3×$$\frac{\sqrt{15}}{4}$=$\frac{3\sqrt{15}}{4}$．
点评 本题主要考查了同角三角函数基本关系式的应用，考查了正弦定理，余弦定理，三角形面积公式在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
19．下列从集合A到集合B的对应f是映射的是（ ）
| A． | A=R，B={x|x是正实数}，f：A中的数的绝对值 | |
| B． | A={0，1}，B={-1，0，1}，f：A中的数的开方 | |
| C． | A=Z，B=Q，f：A中的数的倒数 | |
| D． | A={-1，0，1}，B={-1，0，1}，f：A中的数的平方 |
3．命题P：?x∈R，x2＞lg1，则P的否定￢P为（ ）
| A． | ?x0∈R，${{x}_{0}}^{2}$≤lg1 | B． | ?x0∈R，${{x}_{0}}^{2}$＜lg1 | ||
| C． | ?x∈R，${{x}_{0}}^{2}$≤lg1 | D． | $?{x_{\;}}∈R，x_{\;}^2＜lg1$ |
13．函数f（x）=-x2+3x+a，g（x）=2x-x2，若f（g（x））≥0对x∈[0，1]恒成立，则实数a的取值范围是（ ）
| A． | [-e，+∞） | B． | [-ln2，+∞） | C． | [-2，+∞） | D． | （-$\frac{1}{2}$，0] |
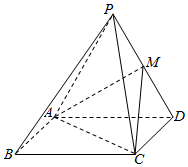如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，且△PAD是边长为4的正三角形，M为PD的中点，底面ABCD是矩形，CD=3．