题目内容
19．下列从集合A到集合B的对应f是映射的是（ ）| A． | A=R，B={x|x是正实数}，f：A中的数的绝对值 | |
| B． | A={0，1}，B={-1，0，1}，f：A中的数的开方 | |
| C． | A=Z，B=Q，f：A中的数的倒数 | |
| D． | A={-1，0，1}，B={-1，0，1}，f：A中的数的平方 |
分析 利用映射概念逐一核对四个命题得答案．
解答 解：对于A，集合A中的元素0取绝对值在B中没有对应元素，故A不是映射；
对于B，集合A中的元素1开方后在B中对应元素不唯一，故B不是映射；
对于C，集合A中的元素0取倒数在B中没有对应元素，故C不是映射；
对于D，集合A中的元素-1，1的平方都是1，0的平方为0，符合映射概念．
故选：D．
点评 本题考查映射概念，是基础题．
练习册系列答案
相关题目
10．
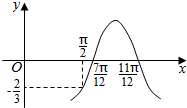已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，f（$\frac{7π}{12}$）=0，f（$\frac{11π}{12}$）=0，则A=（ ）
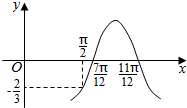已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，f（$\frac{7π}{12}$）=0，f（$\frac{11π}{12}$）=0，则A=（ ）| A． | 1 | B． | x | C． | 0 | D． | $\frac{2}{3}$$\sqrt{2}$ |
9．设x，y满足约束条件$\left\{\begin{array}{l}{x-y≤0}\\{x+2y-6≤0}\\{2x+y-3≥0}\end{array}\right.$，目标函数z=ax-y仅在（0，3）取得最大值，则a的取值范围是（ ）
| A． | （$\frac{1}{2}$，+∞） | B． | （-2，-$\frac{1}{2}$） | C． | （-∞，-$\frac{1}{2}$） | D． | （-∞，-2） |