题目内容
18.圆E:(x+2)2+y2=4,点,动圆P过点F(2,0),且与圆E内切于点M,则动圆P的圆心P的轨迹方程是x2-$\frac{{y}^{2}}{3}$=1(x≤-1).分析 利用动圆与圆E内切于点M,|PF|-|PE|=|ME|=2,可得P的轨迹是以E、F为焦点的双曲线的左支,即可求动圆P的圆心P的轨迹方程.
解答 解:∵圆的方程为E:(x+2)2+y2=4,∴圆心为B(-2,0),半径r=2.
设动圆圆心为P(x,y),依题意,
∵动圆与圆E内切于点M,
∴|PF|-|PE|=|ME|=2,
∴P的轨迹是以E、F为焦点的双曲线的左支,其中2a=2,得a=1,
而c=2,∴b2=c2-a2=3,
∴双曲线方程为:x2-$\frac{{y}^{2}}{3}$=1(x≤-1).
故答案为:x2-$\frac{{y}^{2}}{3}$=1(x≤-1).
点评 本题考查圆与圆的位置关系,考查双曲线的定义与方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
6.“?x∈R,ex-2>m”是“m2>2”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
13.已知函数f(x-1)的定义域是[-1,3],则f(x)=f(2x)+lg(1-x)的定义域为( )
| A. | [-1,1] | B. | [-1,1) | C. | [-4,1) | D. | [-4,1] |
3.已知数列$\sqrt{3}$,$\sqrt{5}$,$\sqrt{7}$,$\sqrt{11}$,…,$\sqrt{2n+1}$,…,则5是这个数列的( )
| A. | 第12项 | B. | 第13项 | C. | 第14项 | D. | 第25项 |
10.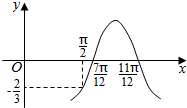 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )
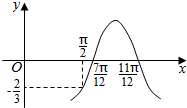 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )| A. | 1 | B. | x | C. | 0 | D. | $\frac{2}{3}$$\sqrt{2}$ |