题目内容
(本小题满分12分)
设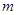 是实数,
是实数,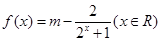 ,
,
(1)若函数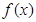 为奇函数,求
为奇函数,求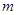 的值;
的值;
(2)试用定义证明:对于任意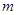 ,
,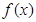 在
在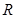 上为单调递增函数;
上为单调递增函数;
(3)若函数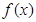 为奇函数,且不等式
为奇函数,且不等式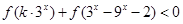 对任意
对任意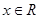 恒成立,求实数
恒成立,求实数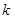 的取值范围。
的取值范围。
设
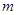 是实数,
是实数,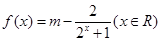 ,
,(1)若函数
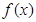 为奇函数,求
为奇函数,求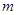 的值;
的值;(2)试用定义证明:对于任意
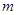 ,
,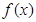 在
在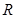 上为单调递增函数;
上为单调递增函数;(3)若函数
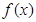 为奇函数,且不等式
为奇函数,且不等式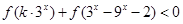 对任意
对任意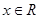 恒成立,求实数
恒成立,求实数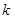 的取值范围。
的取值范围。(1) m="1"
(2)根据函数单调性,结合定义设出变量,结合作差法得到,变形得到证明。
(3)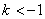
(2)根据函数单调性,结合定义设出变量,结合作差法得到,变形得到证明。
(3)
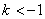
试题分析:解:(1)∵
 ,且
,且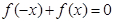
∴
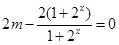 (注:通过
(注:通过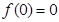 求也同样给分) 3分
求也同样给分) 3分(2)证明:设
 ,则
,则
=
 =
=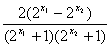
 ,
,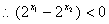
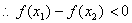 即
即 ,所以
,所以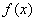 在R上为增函数。 3分
在R上为增函数。 3分(3)因为
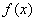 为奇函数且在R上为增函数,
为奇函数且在R上为增函数,由
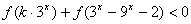 得
得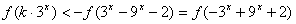
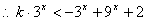 即
即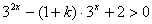 对任意
对任意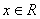 恒成立。
恒成立。令
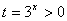 ,问题等价于
,问题等价于 对任意
对任意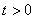 恒成立。
恒成立。令
 ,其对称轴
,其对称轴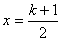 。
。当
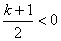 即
即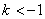 时,
时,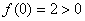 ,符合题意 6分
,符合题意 6分点评:解决的关键是理解奇函数在x=0处函数值为零,同时能结合函数定义来证明函数单调性,确定结论,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
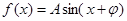 (A>0)在
(A>0)在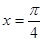 处取最大值,则 ( )
处取最大值,则 ( )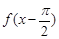 一定是奇函数
一定是奇函数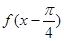 一定是偶函数
一定是偶函数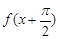 一定是奇函数
一定是奇函数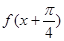 一定是偶函数
一定是偶函数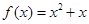 ,
,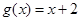 ,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且
,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且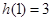 ,则函数h (x)="__________."
,则函数h (x)="__________." 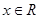 .
.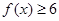 的解集;
的解集;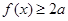 对
对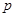 与死亡年数
与死亡年数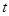 之间的函数关系式;
之间的函数关系式;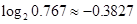 )
)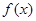 是定义在
是定义在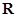 上的偶函数,
上的偶函数,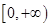 上为增函数,且
上为增函数,且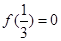 ,则不等式
,则不等式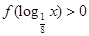 的解集为 .
的解集为 .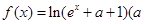 为常数)是实数集
为常数)是实数集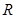 上的奇函数,函数
上的奇函数,函数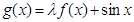 在区间
在区间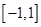 上是减函数.
上是减函数.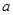 的值;
的值;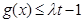 在
在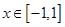 上恒成立,求实数
上恒成立,求实数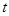 的最大值;
的最大值;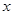 的方程
的方程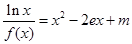 有且只有一个实数根,求
有且只有一个实数根,求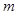 的值.
的值.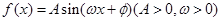 在
在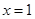 处取得最大值,则( )
处取得最大值,则( ) 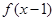 一定是奇函数
一定是奇函数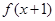 一定是奇函数
一定是奇函数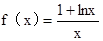
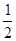 )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围;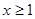 时,不等式
时,不等式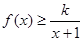 恒成立,求实数
恒成立,求实数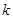 的取值范围。
的取值范围。