题目内容
若函数 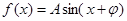 (A>0)在
(A>0)在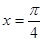 处取最大值,则 ( )
处取最大值,则 ( )
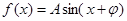 (A>0)在
(A>0)在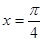 处取最大值,则 ( )
处取最大值,则 ( )A.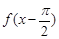 一定是奇函数 一定是奇函数 | B.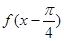 一定是偶函数 一定是偶函数 |
C.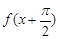 一定是奇函数 一定是奇函数 | D.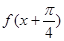 一定是偶函数 一定是偶函数 |
D
试题分析:根据题意可知 ,函数
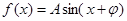 (A>0)在
(A>0)在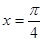 处取最大值,说明了当
处取最大值,说明了当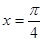 ,则
,则 ,则可知
,则可知 ,那么逐一的进行判定可知
,那么逐一的进行判定可知 选项A,由于
选项A,由于 ,不是奇函数,选项C
,不是奇函数,选项C 不具有奇偶性,选项B
不具有奇偶性,选项B 是奇函数,故选D.
是奇函数,故选D.点评:解决的关键是通过性质确定解析式,进而分析其性质,属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
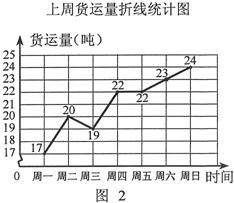
 汽(元)和
汽(元)和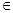 R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )
R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )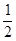
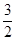
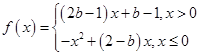 在
在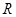 上为增函数,则实数
上为增函数,则实数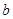 的取值范围为( )
的取值范围为( )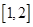
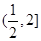
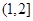
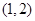
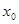 附近的左侧
附近的左侧 ,右侧
,右侧 ,那么
,那么 是极大值
是极大值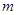 是实数,
是实数,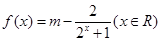 ,
,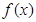 为奇函数,求
为奇函数,求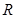 上为单调递增函数;
上为单调递增函数;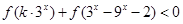 对任意
对任意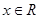 恒成立,求实数
恒成立,求实数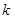 的取值范围。
的取值范围。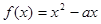 ,
,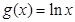
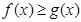 对于定义域内的
对于定义域内的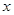 恒成立,求实数
恒成立,求实数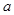 的取值范围;
的取值范围;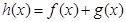 有两个极值点
有两个极值点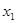 ,
,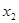 且
且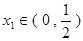 ,求证:
,求证: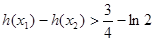 ;
;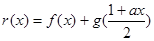 若对任意的
若对任意的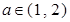 ,总存在
,总存在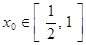 ,使不等式
,使不等式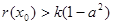 成立,求实数
成立,求实数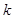 的取值范围.
的取值范围. 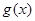 与
与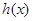 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间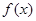 的表达式;
的表达式;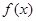 与函数
与函数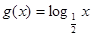 的图像关于直线
的图像关于直线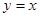 对称,则函数
对称,则函数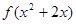 的单调递增区间是
的单调递增区间是