题目内容
8.方程x2+(m+3)x-m=0有两个正实根,则m的取值范围是(-∞,-9].分析 根据一元二次方程方程根的符号,利用根与系数之间的关系即可得到结论.
解答 解:设方程的两个正根分别为x1,x2,
则由根与系数之间的关系可得$\left\{\begin{array}{l}{(m+3)^{2}+4m≥0}\\{-m-3>0}\\{-m>0}\end{array}\right.$,
解得m≤-9,
故m的取值范围为:[-∞,-9];
故答案为:(-∞,-9].
点评 本题主要考查一元二次方程根的根的应用,根据根与系数之间的关系是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.设M={x|x=a2+1,a∈R},P={y|y=b2-4b+5,b∈R},则下列关系正确的是( )
| A. | M=P | B. | M?P | ||
| C. | P?M | D. | M与P没有公共元素 |
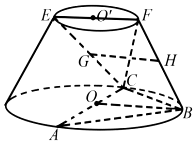 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.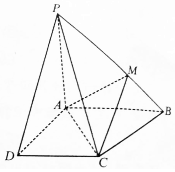 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠BAD=∠ADC=$\frac{π}{2}$,AB=AD=AP=3,DC=2,点M在PB上,且PM=2MB.