题目内容
18.在△ABC中,若A=120°,a=2,b=$\frac{2\sqrt{3}}{3}$,则B=30° .分析 根据正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$即可求解B的大小.
解答 解:由题意A=120°,a=2,b=$\frac{2\sqrt{3}}{3}$,
正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,可得:$\frac{2}{sin120°}=\frac{\frac{2\sqrt{3}}{3}}{sinB}$,解得:sinB=$\frac{1}{2}$.
∵A=120°,
∴B<60°.
∴B=30°.
故答案为30°
点评 本题主要考擦了正弦定理的运用.比较基础.

练习册系列答案
相关题目
9.函数$f(x)={log_2}({{x^2}-x})$的定义域为( )
| A. | [0,1] | B. | (0,1) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,0)∪(1,+∞) |
6.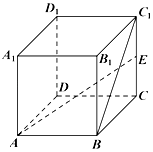 长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )
长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )
 长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )
长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{30}}{10}$ | C. | $\frac{2\sqrt{15}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
13.下列命题正确的是( )
| A. | 对于任意向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$ | |
| B. | 若向量$\overrightarrow{a}$与$\overrightarrow{b}$同向,且|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$. | |
| C. | 向量$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,则A、B、C、D四点一定共线 | |
| D. | 单位向量的模都相等 |
3.为了求函数f(x)=2x+3x-7的一个零点(精确度0.05),某同学已经利用计算器得f(1.5)=0.32843,f(1.25)=-0.8716,则还需用二分法等分区间的次数为( )
| A. | 2次 | B. | 3次 | C. | 4次 | D. | 5次 |
7.执行如图的程序框图,那么输出S的值是( )


| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |