题目内容
9.已知向量|$\overrightarrow{a}$|=1,$\overrightarrow{b}$=(1,$\sqrt{3}$),若2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=0.分析 由已知2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,求出$\overrightarrow{a}•\overrightarrow{b}$,然后利用数量积公式求夹角.
解答 解:因为2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,所以(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=$2\overrightarrow{a}•\overrightarrow{b}-{\overrightarrow{b}}^{2}$=0,
所以$\overrightarrow{a}•\overrightarrow{b}$=2,所以cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{2}{1×2}$=1,
所以<$\overrightarrow{a}$,$\overrightarrow{b}$>=0;
故答案为:0
点评 本题考查了平面向量的数量积公式求向量的夹角;用到了向量垂直,数量积为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知△ABC中,BC=1,A=120°,∠B=θ,记f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$,
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
20.当实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$时,目标函数z=ax+y的最大值为3,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
 如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.
如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.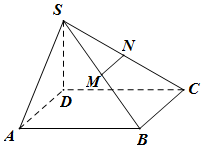 已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q. 如图,直三棱柱的主视图是边长为2的正方形,且俯视图为一个等边三角形,则该三棱柱的左视图面积为2$\sqrt{3}$.
如图,直三棱柱的主视图是边长为2的正方形,且俯视图为一个等边三角形,则该三棱柱的左视图面积为2$\sqrt{3}$.