题目内容
演绎推理“因为对数函数y=logax(a>0且a≠1)是增函数,而函数y=log
x是对数函数,所以y=log
x是增函数”所得结论错误的原因是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、大前提和小前提都错误 |
考点:演绎推理的基本方法
专题:综合题,推理和证明
分析:对数函数的底数的范围不同,则函数的增减性不同,当a>1时,函数是一个增函数,当0<a<1时,对数函数是一个减函数,对数函数y=logax(a>0且a≠1)是增函数这个大前提是错误的.
解答:
解:∵当a>1时,函数y=logax(a>0且a≠1)是一个增函数,
当0<a<1时,此函数是一个减函数
∴y=logax(a>0且a≠1)是增函数这个大前提是错误的,
从而导致结论错.
故选C.
当0<a<1时,此函数是一个减函数
∴y=logax(a>0且a≠1)是增函数这个大前提是错误的,
从而导致结论错.
故选C.
点评:本题考查演绎推理的基本方法,考查对数函数的单调性,解题的关键是理解函数的单调性,分析出大前提是错误的.

练习册系列答案
相关题目
过双曲线C:
-
=1(a>0,b>0)的右顶点作x轴的垂线与C的一条渐近线相交于A.若以C的右焦点为圆心、半径为2的圆经过A、O两点(O为坐标原点),则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、x2-
| ||||
B、x2-
| ||||
C、
| ||||
D、
|
若α为第三象限角,则下列各式中不成立的是 ( )
| A、tanα-sinα<0 |
| B、sinα+cosα<0 |
| C、cosα-tanα<0 |
| D、tanαsinα<0 |
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )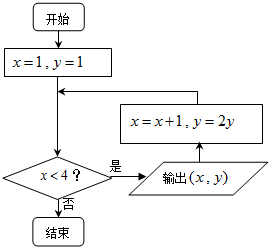

| A、f(x)=log2(x+1)的图象上 | ||
| B、f(x)=x2-2x+2的图象上 | ||
C、f(x)=
| ||
| D、f(x)=2x-1的图象上 |