题目内容
（2x+1）4的展开式中含x的奇次方项的系数和等于（ ）
| A、44 | B、25 | C、41 | D、40 |
考点：二项式系数的性质
专题：计算题,二项式定理
分析：设f（x）=（2x+1）4=a0+a1x+a2x2+a3x3+a4x4，x分别赋值1，-1，可得两个等式，两式相减，再除以2得到答案．
解答：
解：设f（x）=（2x+1）4=a0+a1x+a2x2+a3x3+a4x4，
令x=1，则a0+a1+a2+a3+a4=f（1）=34=81，①
令x=-1，则a0-a1+a2-a3+a4=f（-1）=1．②
①-②得，2（a1+a3）=80，所以奇次项系数之和为40．
故选：D．
令x=1，则a0+a1+a2+a3+a4=f（1）=34=81，①
令x=-1，则a0-a1+a2-a3+a4=f（-1）=1．②
①-②得，2（a1+a3）=80，所以奇次项系数之和为40．
故选：D．
点评：本题考查解决展开式的系数和问题时，一般先设出展开式，再用赋值法代入特殊值，相加或相减．
练习册系列答案
阅读快车系列答案
相关题目
过双曲线
-
=1，（a＞0，b＞0）的右焦点F作垂直于x轴的直线，交双曲线的渐近线于A、B两点，若△OAB（O为坐标原点）是等边三角形，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
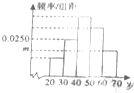为了“城市品位、方便出行、促进发展”，近年合肥市正在修建地铁1号线，市某部门问卷调查了n个市民，其中赞城修建地铁的市民占80%，在赞城修建地铁的市民中又按年龄分组，得样本频率分布直方图如图，其中年龄在[30，40]岁的有2500人，年龄在[60，70）岁的有2000人，则m，n的值分别为（ ）| A、0.2，12500 |
| B、0.2，10000 |
| C、0.02，12500 |
| D、0.02，10000 |
下列说法错误的是（ ）
| A、两两相交且不过同一点的三条直线必在同一平面内 |
| B、过直线外一点有且只有一个平面与已知直线垂直 |
| C、如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直 |
| D、如果两条直线和一个平面所成的角相等，则这两条直线一定平行 |
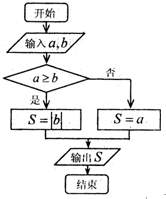
执行如图所示的程序框图，则输出S的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
定义某种运算?，a?b的运算原理如图所示：设f（x）=（0?x）x，则f（x）在区间[-2，2]上的最小值为（ ）| A、-2 | B、-4 | C、2 | D、-8 |
下列命题中是假命题的是（ ）
| A、?a，b∈R*，lg（a+b）≠lga+lgb |
| B、?φ∈R，使得函数f（x）=sin（2x+φ）是偶函数 |
| C、?α，β∈R，使得cos（α+β）=cosα+cosβ |
| D、?m∈R，使f（x）=（m-1）•x m2-2m+3是幂函数，且在（0，+∞）上递减 |
已知函数f（x）=
满足对任意x1≠x2，都有
＞0 成立，则a的取值范围是（ ）
|
| f(x1)-f(x2) |
| x1-x2 |
| A、（1，2] | ||
| B、（1，2） | ||
C、（
| ||
D、[
|