题目内容

11．已知命题p：?x0∈R，x02＜x0，命题q：?x∈R，x2-x+1＞0，则下列命题中为真命题的是（　　）
A．p∧qB．p∧￢qC．￢p∧qD．￢p∧￢q

分析 分别判断出p，q的真假，从而判断出复合命题的真假即可．

解答 解：命题p：?x0∈R，x02＜x0，
如x0=0.1，成立，
故命题p是真命题；
命题q：?x∈R，x2-x+1${（x-\frac{1}{2}）}^{2}$+$\frac{3}{4}$＞0，
故命题q是真命题，
故p∧q是真命题，
故选：A．

点评 本题考查了不等式问题，考查复合命题的判断，是一道基础题．

练习册系列答案
相关题目
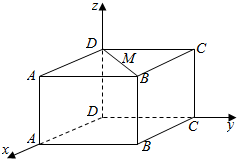1．在如图所示的长方体ABCD-A1B1C1D1中，|DA|=8，|DC|=6，|DD1|=3，则D1B1的中点M的坐标为（4，3，3），|DM|=$\sqrt{34}$．
2．以下几个命题中：其中真命题的序号为③④（写出所有真命题的序号）
①设A，B为两点定点，k为非零常数，|$\overrightarrow{PA}$|-|$\overrightarrow{PB}$|=k，则动点P的轨迹为双曲线；
②过定圆C上一定点A作圆的动弦AB，O为坐标原点，若$\overrightarrow{OP}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$则动点P的轨迹为椭圆；
③双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1$与椭圆$\frac{{x}^{2}}{35}+{y}^{2}$=1有相同的焦点；
④若方程2x2-5x+a=0的两根可分别作为椭圆和双曲线的离心率，则0＜a＜3；
⑤在平面内，到定点（2，1）的距离与到定直线3x+4y-10=0的距离相等的点的轨迹是抛物线．
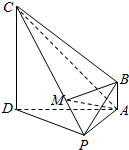19．在四棱锥P-ABCD中，CD⊥平面PAD，AB∥CD，AD⊥PA，△ADC、△PAD均为等腰三角形，AD=4AB=4，M为线段CP上一点，且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$（0≤λ≤1）．
（1）若λ=$\frac{1}{4}$，求证：MB∥平面PAD；并求M到平面ABCD的距离；
（2）若λ=$\frac{1}{8}$，求二面角C-AB-M的余弦值．
6．已知关于x的不等式|2x+a|＜b的解集为{x|1＜x＜2}．
（1）求实数a，b的值；
（2）求函数f（x）=2|x-a|+|x+b|的最小值．
3．当x＞0时，x2+mx+1≥0恒成立，且关于t的不等式t2+2t+m≤0有解，则实数m的取值范围是（　　）
A．[1，+∞）B．[-2，1]C．（-∞，-2]∪[1，+∞）D．（-∞，-2]
20．在直角坐标平面上，已知长轴为6的椭圆C与抛物线D有共同的焦点F1（-2，0）．
（1）求椭圆C与抛物线D的标准方程；
（2）已知椭圆C与抛物线D相交于A、B两点，求△ABF1的面积S${\;}_{△AB{F}_{1}}$．
1．在△ABC中，a=1，B=45°，S△ABC=2，则b=5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网