题目内容
20.(1+tan18°)(1+tan27°)的值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 要求的式子即 1+tan18°+tan27°+tan18°tan27°,再把tan18°+tan27°=tan45°(1-tan18°tan27°)代入,化简可得结果.
解答 解:(1+tan18°)(1+tan27°)
=1+tan18°+tan27°+tan18°tan27°
=1+tan45°(1-tan18°tan27°)+tan18°tan27°
=2,
故选C.
点评 本题主要考查两角和差的正切公式的应用,属于基础题.

练习册系列答案
相关题目
9.在如表数表中,已知每行、每列中的数都成等差数列,那么,位于表中的第n行、第(n+1)列的数是( )
| 第1列 | 第2列 | 第3列 | … | |
| 第1行 | 1 | 2 | 3 | … |
| 第2行 | 2 | 4 | 6 | … |
| 第3行 | 3 | 6 | 9 | … |
| … | … | … | … | … |
| A. | n2-n+1 | B. | n2-n | C. | n2+n | D. | n2+n+2 |
10.若f′(x)是f(x)的导函数,f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e,则f(lnx)<x2的解集为( )
| A. | (0,$\frac{e}{2}$) | B. | ($\frac{e}{2}$,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | (0,$\sqrt{e}$) |
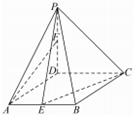 如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.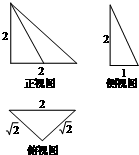 如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.