题目内容
1.已知函数是定义在R上的奇函数,当x>0时,f(x)=-x2-x,则f(-2)=( )| A. | 6 | B. | -6 | C. | 2 | D. | -2 |
分析 利用函数的奇偶性将f(-2)转化为f(-2)=-f(2),然后直接代入解析式即可.
解答 解:∵函数f(x)是定义在R上的奇函数,
∴f(-2)=-f(2),
∵x>0时,f(x)=-x2-x,
∴f(-2)=-f(2)=-(-4-2)=6.
故选A.
点评 本题主要考查函数奇偶性的应用,利用函数的奇偶性将f(-2)转化到已知条件上是解决本题的关键.

练习册系列答案
相关题目
9.在如表数表中,已知每行、每列中的数都成等差数列,那么,位于表中的第n行、第(n+1)列的数是( )
| 第1列 | 第2列 | 第3列 | … | |
| 第1行 | 1 | 2 | 3 | … |
| 第2行 | 2 | 4 | 6 | … |
| 第3行 | 3 | 6 | 9 | … |
| … | … | … | … | … |
| A. | n2-n+1 | B. | n2-n | C. | n2+n | D. | n2+n+2 |
6.已知集合A={x|2x>1},集合B={x|x>m},则“m>0”是“A∪B=A”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为( )
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
10.若f′(x)是f(x)的导函数,f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e,则f(lnx)<x2的解集为( )
| A. | (0,$\frac{e}{2}$) | B. | ($\frac{e}{2}$,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | (0,$\sqrt{e}$) |
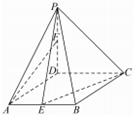 如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,∠BCD=60°,PD⊥平面ABCD,PD=AD=CD=1,点E、F分别为AB和PD的中点.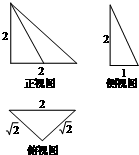 如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.