题目内容
求函数y=3-2sinx取得最大值和最小值时的自变量x的集合．
考点：三角函数的最值
专题：三角函数的求值
分析：利用正弦函数的单调性与最值即可求得函数y=3-2sinx的最大值和最小值．并求取得最大值，最小值时x的集合．
解答：
解：∵-1≤sinx≤1，
∴-2≤-2sinx≤2，
∴1≤3-2sinx≤5，
∴y=3-2sinx的最大值为5，当x=2kπ-
，k∈Z时函数取得最大值．
函数取得最大值时x的集合{x=2kπ-
，k∈Z}．
最小值为1；当x=2kπ+
，k∈Z时函数取得最小值．
函数取得最小值x的集合{x=2kπ+
，k∈Z}．
∴-2≤-2sinx≤2，
∴1≤3-2sinx≤5，
∴y=3-2sinx的最大值为5，当x=2kπ-
| π |
| 2 |
函数取得最大值时x的集合{x=2kπ-
| π |
| 2 |
最小值为1；当x=2kπ+
| π |
| 2 |
函数取得最小值x的集合{x=2kπ+
| π |
| 2 |
点评：本题考查正弦函数的单调性与最值，掌握正弦函数的性质是关键，属于基本知识的考查．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知集合A={-1，2}，B={x|mx+1=0}，若A∩B=B，则所有实数m的值组成的集合是（ ）
| A、{-1，2} | ||
B、{1，-
| ||
C、{1，0，-
| ||
D、{-1，0，
|
已知集合M={x||x|＜2}，N={x|-1≤x≤3}，M∪N=（ ）
| A、{-1，2} |
| B、[-1，2） |
| C、{-2，3} |
| D、（-2，3] |
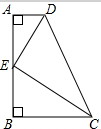如图，在直角梯形ABCD中，AB⊥AD，AB⊥BC，∠BCD与∠ADC的平分线相交于AB上的一点E，以AB为直径作圆，则该圆与边DC有怎样的位置关系？请说明理由．
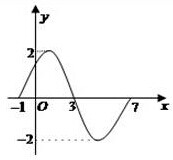如图为函数y1=Asin（ωx+φ）（|φ|＜