题目内容
对任意x∈R,函数f(x)都满足f(x+2)=2f(x),且当x∈[0,2]时,f(x)=x(2-x).则方程f(x)=log4|x|在区间[-4,4]内的解的个数是( )
| A、4 | B、5 | C、6 | D、7 |
考点:对数函数图象与性质的综合应用
专题:数形结合,函数的性质及应用
分析:依题意,在同一坐标系中画出满足条件的函数f(x)与函数y=log4|x|的图象,由图可得答案.
解答:
 解:在同一坐标系中画出满足条件:①定义域为R;
解:在同一坐标系中画出满足条件:①定义域为R;
②?x∈R,有f(x+2)=2f(x);
③当x∈[0,2]时,f(x)=x(2-x)与函数y=log4|x|的图象:
观察图象可得:两个函数的图象共有4个交点
则f(x)=log4|x|在区间[-4,4]内的解个数是4个.
故选:A.
 解:在同一坐标系中画出满足条件:①定义域为R;
解:在同一坐标系中画出满足条件:①定义域为R;②?x∈R,有f(x+2)=2f(x);
③当x∈[0,2]时,f(x)=x(2-x)与函数y=log4|x|的图象:
观察图象可得:两个函数的图象共有4个交点
则f(x)=log4|x|在区间[-4,4]内的解个数是4个.
故选:A.
点评:本题考查根的存在性及根的个数判断,着重考查作图、识图能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A,B的对边分别为a,b,且tanA:tanB=a2:b2,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
下列命题中正确的是( )
| A、20.3<1 | ||||
| B、?m,n∈R+,lg(m+n)=lgm•lgn | ||||
C、4 -
| ||||
D、若3
|
命题“?x∈[1,3],x2-a≤0”为真命题的一个充分不必要条件是( )
| A、a≥9 | B、a≤9 |
| C、a≥10 | D、a≤10 |
已知向量
=(-2,x-2),
=(-1,
),若
∥
,则x的值是( )
| AB |
| CD |
| 1 |
| 2 |
| AB |
| CD |
| A、2 | B、3 | C、4 | D、5 |
阅读图中的程序,则A的输出值为( )


| A、10 | B、15 | C、20 | D、25 |
 如图,已知正三棱锥P-ABC的各棱长均为a,M是棱BC的中心,则PA与MA所成角的余弦值是
如图,已知正三棱锥P-ABC的各棱长均为a,M是棱BC的中心,则PA与MA所成角的余弦值是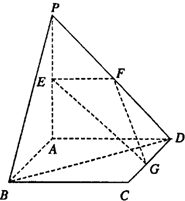 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.