题目内容
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)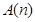 :
: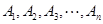 与
与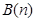 :
: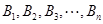 ,其中
,其中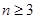 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段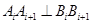 ,其中
,其中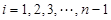 ,则称
,则称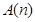 与
与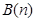 互为正交点列.
互为正交点列.
(1)求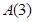 :
: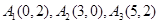 的正交点列
的正交点列 ;
;
(2)判断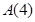 :
: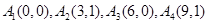 是否存在正交点列
是否存在正交点列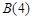 ?并说明理由;
?并说明理由;
(3)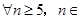 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列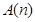 ?并证明你的结论.
?并证明你的结论.
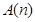 :
: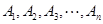 与
与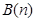 :
: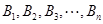 ,其中
,其中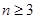 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段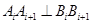 ,其中
,其中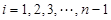 ,则称
,则称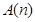 与
与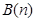 互为正交点列.
互为正交点列.(1)求
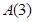 :
: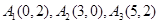 的正交点列
的正交点列 ;
;(2)判断
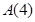 :
: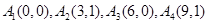 是否存在正交点列
是否存在正交点列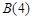 ?并说明理由;
?并说明理由;(3)
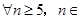 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列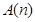 ?并证明你的结论.
?并证明你的结论.(1)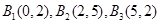 ,(2)不存在,(3)存在.
,(2)不存在,(3)存在.
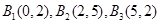 ,(2)不存在,(3)存在.
,(2)不存在,(3)存在.试题分析:(1)因为
 与
与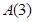 的起点和终点分别相同,所以
的起点和终点分别相同,所以 ,只需求
,只需求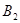 .由
.由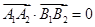 及
及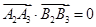 ,可解得
,可解得 本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求
本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求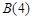 角度出发,能求出来就存在,否则就不存在.首先有
角度出发,能求出来就存在,否则就不存在.首先有 求
求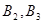 时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即
时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即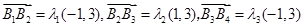 ,因为
,因为 相同,所以有
相同,所以有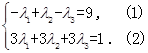 因为
因为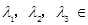
 ,所以方程组显然不成立,即不存在.
,所以方程组显然不成立,即不存在.(3)按照(1)的思路,要保证方程组
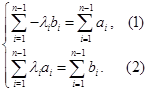 无解,须使得整数尽量取
无解,须使得整数尽量取 ,①当
,①当 为偶数时,取
为偶数时,取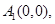
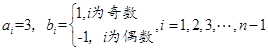 .②当
.②当 为奇数时,取
为奇数时,取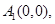
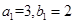 ,
,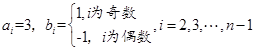 ,就可满足题意.
,就可满足题意.试题解析:解:
(1)设点列
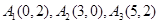 的正交点列是
的正交点列是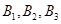 ,
,由正交点列的定义可知
 ,设
,设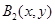 ,
,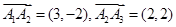 ,
,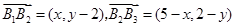 ,
,由正交点列的定义可知
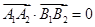 ,
,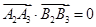 ,
,即
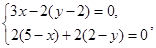 解得
解得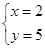
所以点列
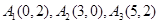 的正交点列是
的正交点列是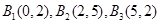 . 3分
. 3分(2)由题可得
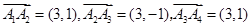 ,
,设点列
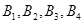 是点列
是点列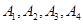 的正交点列,
的正交点列,则可设
 ,
,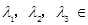

因为
 相同,所以有
相同,所以有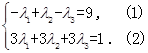
因为
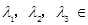
 ,方程(2)显然不成立,
,方程(2)显然不成立,所以有序整点列
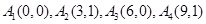 不存在正交点列; 8分
不存在正交点列; 8分(3)
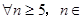
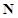 ,都存在整点列
,都存在整点列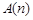 无正交点列. 9分
无正交点列. 9分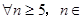
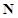 ,设
,设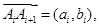 其中
其中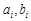 是一对互质整数,
是一对互质整数,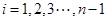
若有序整点列
 是点列
是点列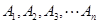 正交点列,
正交点列,则
 ,
,则有
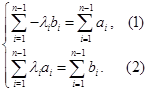
①当
 为偶数时,取
为偶数时,取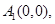
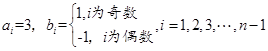 .
.由于
 是整点列,所以有
是整点列,所以有
 ,
, .
.等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列
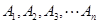 无正交点列;
无正交点列;②当
 为奇数时,
为奇数时,取
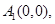
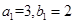 ,
,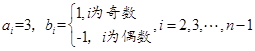 ,
,由于
 是整点列,所以有
是整点列,所以有
 ,
, .
.等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列
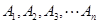 无正交点列.
无正交点列.综上所述,
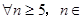
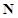 ,都不存在无正交点列的有序整数点列
,都不存在无正交点列的有序整数点列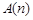 13分
13分
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 =________.
=________. ”为向量
”为向量 与向量
与向量 的“外积”,若向量
的“外积”,若向量 ,它的长度规定为:
,它的长度规定为: ,现已知
,现已知 ,则
,则 ____________.
____________. ,且
,且 与
与 的夹角为
的夹角为 ,当
,当 取得最小值时,实数
取得最小值时,实数 的值为( )
的值为( )

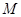 是梯形
是梯形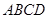 内或边界上的一个动点,点N是DC边的中点,则
内或边界上的一个动点,点N是DC边的中点,则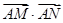 的最大值是________ .
的最大值是________ .
 中,
中, ( )
( ) 



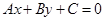 与圆
与圆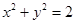 相交于
相交于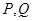 两点,其中
两点,其中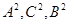 成等差数列,
成等差数列,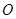 为坐标原点,则
为坐标原点,则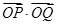 =___________.
=___________. ×
× )·
)·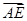 =( )
=( )
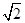
 ,
, ,
, ,且
,且 ,则
,则 .
.