题目内容
对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sin θ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图所示,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则( ×
× )·
)·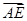 =( )
=( )

 ×
× )·
)·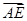 =( )
=( )
| A.4 | B.8 | C.2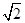 | D.4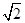 |
D
根据向量积定义知,向量 ×
× 垂直平面ABCD,且方向向上,设
垂直平面ABCD,且方向向上,设 ×
× 与
与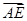 所成角为θ.因为∠EAB=∠EAD=∠BAD=60°,所以点E在底面ABCD上的射影在直线AC上.
所成角为θ.因为∠EAB=∠EAD=∠BAD=60°,所以点E在底面ABCD上的射影在直线AC上.
作EI⊥AC于I,则EI⊥平面ABCD,所以θ+∠EAI= .过I作IJ⊥AD于J,连接EJ,由三垂线逆定理可得EJ⊥AD.因为AE=2,∠EAD=60°,所以AJ=1,EJ=
.过I作IJ⊥AD于J,连接EJ,由三垂线逆定理可得EJ⊥AD.因为AE=2,∠EAD=60°,所以AJ=1,EJ= .又∠CAD=30°,IJ⊥AD,所以AI=
.又∠CAD=30°,IJ⊥AD,所以AI= .因为AE=2,EI⊥AC,所以cos EAI=
.因为AE=2,EI⊥AC,所以cos EAI= =
= ,
,
所以sin θ=sin =cos EAI=
=cos EAI= ,cos θ=
,cos θ= .
.
故( ×
× )·
)·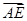 =|
=| ||
|| |sin BAD|
|sin BAD|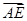 |.
|.
cos θ=8× ×
× =4
=4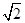 ,故选D.
,故选D.
 ×
× 垂直平面ABCD,且方向向上,设
垂直平面ABCD,且方向向上,设 ×
× 与
与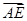 所成角为θ.因为∠EAB=∠EAD=∠BAD=60°,所以点E在底面ABCD上的射影在直线AC上.
所成角为θ.因为∠EAB=∠EAD=∠BAD=60°,所以点E在底面ABCD上的射影在直线AC上.作EI⊥AC于I,则EI⊥平面ABCD,所以θ+∠EAI=
 .过I作IJ⊥AD于J,连接EJ,由三垂线逆定理可得EJ⊥AD.因为AE=2,∠EAD=60°,所以AJ=1,EJ=
.过I作IJ⊥AD于J,连接EJ,由三垂线逆定理可得EJ⊥AD.因为AE=2,∠EAD=60°,所以AJ=1,EJ= .又∠CAD=30°,IJ⊥AD,所以AI=
.又∠CAD=30°,IJ⊥AD,所以AI= .因为AE=2,EI⊥AC,所以cos EAI=
.因为AE=2,EI⊥AC,所以cos EAI= =
= ,
,所以sin θ=sin
 =cos EAI=
=cos EAI= ,cos θ=
,cos θ= .
.故(
 ×
× )·
)·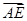 =|
=| ||
|| |sin BAD|
|sin BAD|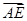 |.
|.cos θ=8×
 ×
× =4
=4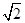 ,故选D.
,故选D.
练习册系列答案
相关题目
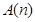 :
: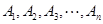 与
与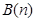 :
: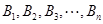 ,其中
,其中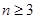 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段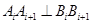 ,其中
,其中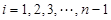 ,则称
,则称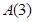 :
: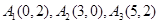 的正交点列
的正交点列 ;
;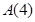 :
: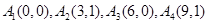 是否存在正交点列
是否存在正交点列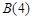 ?并说明理由;
?并说明理由;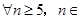 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列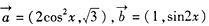 ,函数
,函数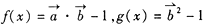
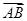 =a,
=a,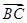 =b,求△ABC的面积.
=b,求△ABC的面积. 、
、 的夹角为
的夹角为 ,且
,且 ,
, ,则向量
,则向量 的夹角等于 .
的夹角等于 .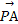 ·
·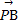 的最小值为( )
的最小值为( )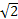
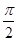
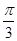
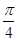
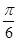
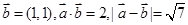 ,则
,则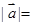 .
.