题目内容
 已知F1、F2为双曲线
已知F1、F2为双曲线| x2 |
| a2 |
| y2 |
| b2 |
| MF1 |
| MF2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:由双曲线的性质得|
|=b,|
|=3b,cos∠F1OM=-
,由此利用余弦定理利用渐近线方程.
| MF2 |
| MF1 |
| a |
| c |
解答:
解:根据题意由双曲线的性质得|
|=b,
则|
|=3b,在△MF1O中,|
|=a,|
|=c,
cos∠F1OM=-
,
由余弦定理可知
=-
,
又c2=a2+b2,得a2=2b2,即
=
,
∴渐近线方程为y=±
x.
故答案为:y=±
x.
| MF2 |
则|
| MF1 |
| OM |
| OF1 |
cos∠F1OM=-
| a |
| c |
由余弦定理可知
| a2+c2-9b2 |
| 2ac |
| a |
| c |
又c2=a2+b2,得a2=2b2,即
| b |
| a |
| ||
| 2 |
∴渐近线方程为y=±
| ||
| 2 |
故答案为:y=±
| ||
| 2 |
点评:本题考查双曲线的渐近线方程的求法,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目

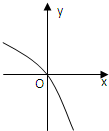 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为