题目内容
已知点A(1,1)、B(-1,5)及
=
,
=2
,
=-
,求C、D、E的坐标.
| AC |
| 1 |
| 2 |
| AB |
| AD |
| AB |
| AE |
| 1 |
| 2 |
| AB |
考点:平行向量与共线向量
专题:平面向量及应用
分析:设C(a,b)、D(c,d)、E(m,n),由题意利用两个向量坐标形式的运算法则,求得C、D、E的坐标.
解答:
解:设C(a,b)、D(c,d)、E(m,n),则由题意可得 (a-1,b-1)=
(-2,4)=(-1,2),
(c-1,d-1)=2(-2,4)=(-4,8),(m-1,n-1)=-
(-2,4)=(1,-2).
求得 a=0,b=3,c=-3,d=9,m=2,n=-1,
可得C(0,3)、D(-3,9)、E(2,-1).
| 1 |
| 2 |
(c-1,d-1)=2(-2,4)=(-4,8),(m-1,n-1)=-
| 1 |
| 2 |
求得 a=0,b=3,c=-3,d=9,m=2,n=-1,
可得C(0,3)、D(-3,9)、E(2,-1).
点评:本题主要考查两个向量的加减法法则,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合B={x|x2≤4},则集合∁RB=( )
| A、(2,+∞) |
| B、[2,+∞) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2]∪[2,+∞) |
已知函数f(x)=x3+ax2-x+c(x∈R),则下列结论错误的是( )
| A、函数f(x)一定存在极大值和极小值 | ||||
B、若f(x)在(-∞,x1)、(x2,+∞)上是增函数,则x2-x1≥
| ||||
| C、函数f(x)在点(x0,f(x0))处的切线与f(x)的图象必有两个不同公共点 | ||||
| D、函数f(x)的图象是中心对称图形 |
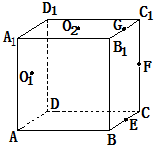 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是