题目内容
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求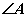 和
和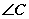 互补,且AB=BC
互补,且AB=BC
(1) 设AB=x米,cosA=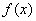 ,求
,求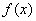 的解析式,并指出x的取值范围.
的解析式,并指出x的取值范围.
(2) 求四边形ABCD面积的最大值.
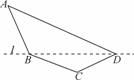
(1)在△ABD中,由余弦定理得BD2=AB2+AD2-2AB·AD·cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB·CD·cosC. 因为∠A和∠C互补,
所以AB2+AD2-2AB·AD·cosA=CB2+CD2-2CB· CD·cosC=CB2+CD2+2CB·CD·
CD·cosC=CB2+CD2+2CB·CD· cosA.
cosA.
即 x2+(9-x)2-2 x(9-x) cosA=x2+(5-x)2+2 x(5-x) cosA.
解得 cosA=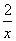 ,即f( x)=
,即f( x)=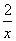 .其中x∈(2,5).
.其中x∈(2,5).
(2)四边形ABCD的面积S=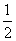 (AB·AD+ CB·CD)sinA=
(AB·AD+ CB·CD)sinA=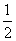 [x(5-x)+x(9-x)]
[x(5-x)+x(9-x)] 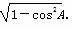 .
.
=x(7-x) 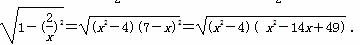
记g(x)=(x2-4)( x2-14x+49),x∈(2,5).
由g′(x)=2x( x2-14x+49)+(x2-4)( 2 x-14)=2(x-7)(2 x2-7 x-4)=0,
解得x=4(x=7和x=-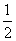 舍).
舍).
所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.所以S的最大值为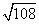 =6
=6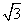 .
.
答:所求四边形ABCD面积的最大值为6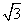 m2.
m2.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
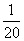 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.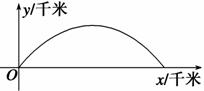
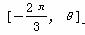 上的最大值为1,
上的最大值为1,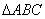 中,∠B=45°,D是BC边上一点,AD=5,AC=7,DC=3,则AB的长为________.
中,∠B=45°,D是BC边上一点,AD=5,AC=7,DC=3,则AB的长为________.
 中设
中设
 的中点为
的中点为 ,
, 的中点为
的中点为 ,
, 的中点恰为
的中点恰为 ,则
,则 = .(用
= .(用 表示)
表示) 若
若 与
与 的夹角为钝角,则x的取值范围为
的夹角为钝角,则x的取值范围为  .
.

 在点(0,1)处的切线方程为 。
在点(0,1)处的切线方程为 。