题目内容
已知m是3和15和等差中项,则曲线
+
=1的离心率为( )
| x2 |
| 16 |
| y2 |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质,等差数列的性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据m是3和15和等差中项,由等差数列的性质得到关于m的方程,求出方程的解得到m的值,进而找出曲线的a与b的值,求出c的值,然后根据离心率的公式即可求出曲线的离心率.
解答:
解:由实数m是3和15和等差中项,得到m=9,
则双曲线方程中的a2=16,b2=9,则c=
,
所以曲线
+
=1的离心率为e=
=
.
故选:B.
则双曲线方程中的a2=16,b2=9,则c=
| 7 |
所以曲线
| x2 |
| 16 |
| y2 |
| m |
| c |
| a |
| ||
| 4 |
故选:B.
点评:此题考查学生掌握等差数列的性质以及椭圆的简单性质,是一道基础题.

练习册系列答案
相关题目
在锐角△ABC中,C=
,则tanA+tanB的最小值为( )
| π |
| 4 |
A、3+2
| ||
B、2+2
| ||
C、2
| ||
D、2
|
执行如图所示的程序框图,则输出的S值是( )


| A、511 | B、255 |
| C、127 | D、63 |
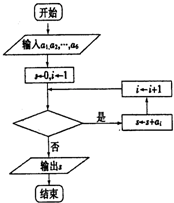 如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填( )
如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填( )| A、i≤5或i<6 |
| B、i≤6或i<7 |
| C、i≥6或i>5 |
| D、i≥5或i>4 |
设θ是△ABC的一个内角,且sinθ+cosθ=
,则x2sinθ+y2cosθ=1表示( )
| 1 |
| 5 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
已知f(x)的图象与函数y=log3(x-1)+9的图象关于直线y=x对称,则f(10)的值为( )
| A、11 | B、12 | C、2 | D、4 |
函数f(x)=2sin(
-x)sin(
+x)(x∈R)是( )
| π |
| 4 |
| π |
| 4 |
| A、最大值为2的偶函数 |
| B、最大值为1的偶函数 |
| C、最大值为2的奇函数 |
| D、最大值为1的奇函数 |