题目内容
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.已知射线l:θ=
与曲线C:
(t为参数)相交于A,B两点.
(1)写出射线l的参数方程和曲线C的直角坐标方程;
(2)求线段AB中点的极坐标.B两点,求|AB|的值.
| π |
| 4 |
|
(1)写出射线l的参数方程和曲线C的直角坐标方程;
(2)求线段AB中点的极坐标.B两点,求|AB|的值.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)由直线l的极坐标直接得到直角坐标方程,进一步转化为参数方程,直角消掉曲线C中的参数t得其直角坐标方程;
(2)联立直线和抛物线方程,求得A,B的坐标,由中点坐标公式求得中点,转化为极坐标,由两点间的距离公式求|AB|.
(2)联立直线和抛物线方程,求得A,B的坐标,由中点坐标公式求得中点,转化为极坐标,由两点间的距离公式求|AB|.
解答:
解:(1)∵射线l:θ=
,
∴其直角坐标方程为y=x(x≥0),则射线l的参数方程为
(t≥0),
由曲线C:
,消掉t得:y=(x-2)2;
(2)由
,得
,
.
令A(1,1),B(4,4).
则线段AB中点的直角坐标为(
,
),极坐标为(
,
).
|AB|=
=3
.
| π |
| 4 |
∴其直角坐标方程为y=x(x≥0),则射线l的参数方程为
|
由曲线C:
|
(2)由
|
|
|
令A(1,1),B(4,4).
则线段AB中点的直角坐标为(
| 5 |
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
| π |
| 4 |
|AB|=
| (4-1)2+(4-1)2 |
| 2 |
点评:本题考查了极坐标与直角坐标的互化,考查了参数方程化普通方程,训练了两点间的距离公式的应用,是基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
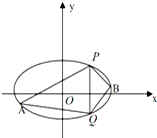 已知椭圆C方程为
已知椭圆C方程为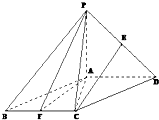 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=