��Ŀ����
19��������R�ϵĺ���f��x������f��x+2��=$\frac{1}{2}$f��x������x��[0��2��ʱ��f��x��=$\left\{\begin{array}{l}{\frac{1}{2}-2{x}^{2}��0��x��1}\\{-{2}^{1-|x-\frac{3}{2}|}��1��x��2}\end{array}\right.$������g��x��=��2x-x2��ex+m����?x1��[-4��-2����?x2��[-1��2]��ʹ�ò���ʽf��x1��-g��x2����0��������ʵ��m��ȡֵ��Χ�ǣ�������| A�� | ��-�ޣ�-8] | B�� | ��-�ޣ�$\frac{3}{e}$+8] | C�� | [$\frac{3}{e}$-8��+�ޣ� | D�� | ��-�ޣ�$\frac{3}{e}$-8] |
���� ��f��x+2��=$\frac{1}{2}$f��x����f��-$\frac{1}{2}$��=2f��$\frac{3}{2}$��=2����-2��=-4��x��[-4��-3]��f��-$\frac{5}{2}$��=2f��-$\frac{1}{2}$��=-8��?x1��[-4��2����f��x1����С=-8�������������g��t����С������ʽf��x1��-g��x2����0��������ó�f��x1����С��g��x2����С����⼴�ɣ�
��� �⣺�ߵ�x��[0��2��ʱ��f��x��=$\left\{\begin{array}{l}\frac{1}{2}-2{x^2}��\;0��x��1\\-\;{2^{1-\;|\;x\;-\;\;\frac{3}{2}\;|}}��\;\;1��x��2.\end{array}\right.$��
��x��[0��2����f��0��=$\frac{1}{2}$Ϊ���ֵ��
��f��x+2��=$\frac{1}{2}$f��x����
��f��x��=2f��x+2����
��x��[-2��0]��
��f��-2��=2f��0��=2��$\frac{1}{2}$=1��
��x��[-4��-3]��
��f��-4��=2f��-2��=2��1=2��
��?x1��[-4��2����
��f��x1�����=2��
��f��x��=2f��x+2����
x��[-2��0]��
��f��-$\frac{1}{2}$��=2f��$\frac{3}{2}$��=2����-2��=-4��
��x��[-4��-3]��
��f��-$\frac{5}{2}$��=2f��-$\frac{1}{2}$��=-8��
��?x1��[-4��2����
��f��x1����С=-8��
�ߺ���g��x��=��2x-x2��ex+m��
��g�䣨x��=��2-x2��ex��
��g�䣨x��=��2-x2��ex=0����2-x2=0��
��x=$\sqrt{2}$����x=-$\sqrt{2}$��
��-1��x��$\sqrt{2}$ʱ��g�䣨x����0��
��$\sqrt{2}$��x��2ʱ��g�䣨x����0��
��g��2��=m��g��-1��=-$\frac{3}{e}$+m��
��x2��[-1��2]ʱ��
g��x2����С=g��-1��=-$\frac{3}{e}$+m��
�߲���ʽ��ʽf��x1��-g��x2����0������
��-8��-$\frac{3}{e}$+m��
��ʵ�����㣺m��$\frac{3}{e}$-8��
��ѡ��D��
���� ���⿼���˺�����ֵ���Լ�ͼ���Ӧ�ã��ж����ֵ����Сֵ���⣬�����������ʹ��������⣬��������ת����������ֵ�ǽ������Ĺؼ����ۺ��Խ�ǿ���ѶȽϴ�

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�| A�� | y=x2+1 | B�� | y=ex-e-x | C�� | y=lg|x| | D�� | $y=\sqrt{x^2}$ |
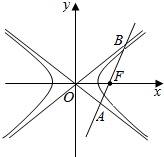 ��ͼ��˫���ߵ�����������ԭ��O��������x���ϣ����������߷ֱ�Ϊ11��12�������ҽ���F��ֱ��11��ֱ�߷ֱ�11��12��A��B���㣬��|$\overrightarrow{OA}$|��|$\overrightarrow{AB}$|��|$\overrightarrow{OB}$|���γɵȲ����У����˫���ߵ�������Ϊ��������
��ͼ��˫���ߵ�����������ԭ��O��������x���ϣ����������߷ֱ�Ϊ11��12�������ҽ���F��ֱ��11��ֱ�߷ֱ�11��12��A��B���㣬��|$\overrightarrow{OA}$|��|$\overrightarrow{AB}$|��|$\overrightarrow{OB}$|���γɵȲ����У����˫���ߵ�������Ϊ��������| A�� | $\frac{\sqrt{5}}{2}$ | B�� | $\sqrt{2}$ | C�� | 2 | D�� | $\sqrt{5}$ |
| A�� | 3$\sqrt{3}$ | B�� | 2$\sqrt{3}$ | C�� | 6 | D�� | 5 |