题目内容
16.(x2-3x+3)3的展开式中,x项的系数为-81.分析 (x2-3x+3)3的展开式的通项公式Tr+1=${∁}_{3}^{r}$×33-r(x2-3x)r,(x2-3x)r的通项公式Tk+1=${∁}_{r}^{k}(-3)^{k}{x}^{2r-k}$,令2r-k=1,r=0,1,2,3,k≤r,k∈N*.解得r=k=1,即可得出.
解答 解:(x2-3x+3)3的展开式的通项公式Tr+1=${∁}_{3}^{r}$×33-r(x2-3x)r,
(x2-3x)r的通项公式Tk+1=${∁}_{r}^{k}({x}^{2})^{r-k}(-3x)^{k}$=${∁}_{r}^{k}(-3)^{k}{x}^{2r-k}$,
令2r-k=1,r=0,1,2,3,k≤r,k∈N*.
∴r=k=1,
∴x项的系数=${∁}_{3}^{1}×{3}^{2}$×${∁}_{1}^{1}(-3)^{1}$=-81.
故答案为:-81.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.某人打算制定一个长期储蓄计划,每年年初存款2万元,连续储蓄12年.由于资金原因,从第7年年初开始,变更为每年年初存款1万元.若存款利率为每年2%,且上一年年末的本息和共同作为下一年年初的本金,则第13年年初时的本息和约为( )万元(结果精确到0.1).(参考数据:1.026≈1.13,1.0212≈1.27)
| A. | 20.09万元 | B. | 20.50万元 | C. | 20.91万元 | D. | 21.33万元 |
7.《九章算术》中“竹九节”问题:现有一根9节的竹子,自上而下各节的容积称等比数列,上面3节的容积共2升,下面3节的容积共128升,则第5节的容积为( )
| A. | 3升 | B. | $\frac{31}{6}$升 | C. | 4升 | D. | $\frac{32}{7}$ |
11.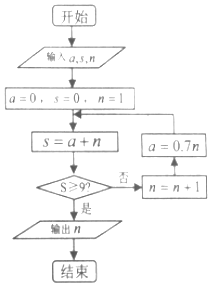 我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
 我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.E为正四面体D-ABC棱AD的中点,平面α过点A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,则m、n所成角的余弦值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{3}$ |
5.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1,F2,直线l经过点F1及虚轴的一个端点,且点F2到直线l的距离等于实半轴的长,则双曲线的离心率为( )
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{4}$ | C. | $\sqrt{\frac{{1+\sqrt{5}}}{2}}$ | D. | $\frac{{\sqrt{3+\sqrt{5}}}}{2}$ |