题目内容
已知二次函数 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点 到点
到点 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
解析 (1)由于
令
①当 ,即
,即 时,
时,  恒成立.
恒成立.
 在(-∞,0)及(0,+∞)上都是增函数.
在(-∞,0)及(0,+∞)上都是增函数.
②当 ,即
,即 时
时

由 得
得 或
或
 或
或 或
或
又由 得
得
综上①当 时,
时, 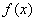 在
在 上都是增函数.
上都是增函数.
②当 时,
时, 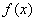 在
在 上是减函数,
上是减函数,

在 上都是增函数.
上都是增函数.
(2)当 时,由(1)知
时,由(1)知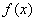 在
在 上是减函数.
上是减函数.
在 上是增函数.
上是增函数.
又



 函数
函数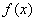 在
在 上的值域为
上的值域为

练习册系列答案
相关题目
 中设
中设
 的中点为
的中点为 ,
, 的中点为
的中点为 ,
, 的中点恰为
的中点恰为 ,则
,则 = .(用
= .(用 表示)
表示)
 中,若
中,若 ,
, ,则
,则 的值是 .
的值是 . 在
在 处取极值,则
处取极值,则
 在点(0,1)处的切线方程为 。
在点(0,1)处的切线方程为 。 的单调递增区间是 ( )
的单调递增区间是 ( ) B.(0,3) C.(1,4) D.
B.(0,3) C.(1,4) D. 
 满足2x+
满足2x+ =5,
=5,  满足2x+2
满足2x+2 (x-1)=5,
(x-1)=5,  = ( )
= ( ) B.
B. 3 C.
3 C. D.4
D.4 满足
满足 ,则其前
,则其前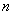 项和
项和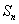 = .
= .