题目内容
若第一象限内的动点P(x,y)满足
+
+
=1,R=xy,则以P为圆心R为半径且面积最小的圆的方程为 .
| 1 |
| x |
| 1 |
| 2y |
| 3 |
| 2xy |
考点:基本不等式
专题:不等式的解法及应用,直线与圆
分析:利用基本不等式可得1=
+
+
≥2
+
,化为(
)2-2
-3≥0,
≥3,
即xy≥
,当且仅当x=2y=3时取等号.即可得到圆心和半径.
| 1 |
| x |
| 1 |
| 2y |
| 3 |
| 2xy |
|
| 3 |
| 2xy |
| 2xy |
| 2xy |
| 2xy |
即xy≥
| 9 |
| 2 |
解答:
解:∵x,y>0,
∴1=
+
+
≥2
+
,化为(
)2-2
-3≥0,当且仅当x=2y=3时取等号.
变为(
-3)(
+1)≥0,
解得
≥3,
即xy≥
,当且仅当x=2y=3时取等号.
∴圆心为(3,
),半径R=xy=
时,以P为圆心R为半径的圆的面积最小.
此时圆的方程为:(x-3)2+(y-
)2=
.的方程为:(x-3)2+(y-
)2=
.
∴1=
| 1 |
| x |
| 1 |
| 2y |
| 3 |
| 2xy |
|
| 3 |
| 2xy |
| 2xy |
| 2xy |
变为(
| 2xy |
| 2xy |
解得
| 2xy |
即xy≥
| 9 |
| 2 |
∴圆心为(3,
| 3 |
| 2 |
| 9 |
| 2 |
此时圆的方程为:(x-3)2+(y-
| 3 |
| 2 |
| 81 |
| 4 |
| 3 |
| 2 |
| 81 |
| 4 |
点评:本题考查了基本不等式的性质、圆的方程,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x3+(b-|a|)x2+(a2-4b)x是奇函数,则f′(0)的最小值是( )
| A、-4 | B、0 | C、1 | D、4 |
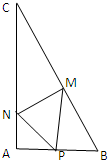 在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是
在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是