题目内容
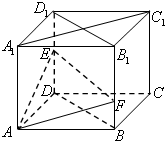
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.(1)求证:EF⊥A1C1;
(2)求几何体ABFED的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)连结B1D1,BD,由已知条件推导出A1C1⊥DD1,从而得到A1C1⊥平面BB1D1D.由此能证明EF⊥A1C1.
(2)求出梯形BDEF的面积,即可求几何体ABFED的体积.
(2)求出梯形BDEF的面积,即可求几何体ABFED的体积.
解答:
(1)证明:连结B1D1,BD,∵四边形A1B1C1D1是正方形,∴B1D1⊥A1C1.
 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:连接AC交BD于点O,由于ABCD-A1B1C1D1为正方体,
∴AA1∥BB1,AA1=BB1,BB1∥CC1,BB1=CC1,AA1∥CC1,AA1=CC1,
∴四边形AA1C1C为平行四边形,AC∥A1C1,AC=A1C1
由(1)知,A1C1⊥平面BB1D1D,∴AC⊥平面BB1D1D,∴AO⊥平面BB1D1D,
由AC=
=
=
a,
∴AO=
AC=
a,
在直角梯形BDEF中,直角腰BD=AC=
a,上底BF=
BB1=
a,下底DE=
DD1=
a,
因此梯形BDEF的面积SBDEF=
(BF+DE)•BD=
×(
+
)×
a=
a2,
因此几何体ABFED的体积VABFED=
AO•SBDEF=
×
a×
a2=
a3.
 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:连接AC交BD于点O,由于ABCD-A1B1C1D1为正方体,
∴AA1∥BB1,AA1=BB1,BB1∥CC1,BB1=CC1,AA1∥CC1,AA1=CC1,
∴四边形AA1C1C为平行四边形,AC∥A1C1,AC=A1C1
由(1)知,A1C1⊥平面BB1D1D,∴AC⊥平面BB1D1D,∴AO⊥平面BB1D1D,
由AC=
| AB2+BC2 |
| a2+a2 |
| 2 |
∴AO=
| 1 |
| 2 |
| ||
| 2 |
在直角梯形BDEF中,直角腰BD=AC=
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
因此梯形BDEF的面积SBDEF=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 3 |
| a |
| 2 |
| 2 |
5
| ||
| 12 |
因此几何体ABFED的体积VABFED=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
5
| ||
| 12 |
| 5 |
| 36 |
点评:本小题主要考查空间线面关系与几何体体积的计算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线将边长为2的正方形折起来,围成一个三棱锥,则此三棱锥的体积是
如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线将边长为2的正方形折起来,围成一个三棱锥,则此三棱锥的体积是