题目内容
已知椭圆x2+
=1的左,右两个顶点分别为A、B.曲线C是以A、B两点为顶点,离心率为
的双曲线.设点P在第一象限且在曲线C上,直线AP与椭圆相交于另一点T.
(1)求曲线C的方程;
(2)设P、T两点的横坐标分别为x1、x2,证明:x1•x2=1.
| y2 |
| 4 |
| 5 |
(1)求曲线C的方程;
(2)设P、T两点的横坐标分别为x1、x2,证明:x1•x2=1.
考点:轨迹方程,直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)依题意设双曲线C的方程,利用双曲线的离心率为
,建立等式,从而可求双曲线C的方程;
(2)设直线AP的方程与椭圆方程联立,确定P、T的横坐标,即可证得结论
| 5 |
(2)设直线AP的方程与椭圆方程联立,确定P、T的横坐标,即可证得结论
解答:
(1)解:依题意可得A(-1,0),B(1,0).…(1分)
设双曲线C的方程为x2-
=1(b>0),
因为双曲线的离心率为
,所以
=
,即b=2.
所以双曲线C的方程为x2-
=1.…(3分)
(2)证明:设点P(x1,y1)、T(x2,y2)(xi>0,yi>0,i=1,2),直线AP的斜率为k(k>0),
则直线AP的方程为y=k(x+1),…(4分)
代入椭圆方程整理,得(4+k2)x2+2k2x+k2-4=0,
解得x=-1或x=
.
所以x2=
..…(6分)
同理可得,x1=
.…(7分)
所以x1•x2=1.…(8分)
设双曲线C的方程为x2-
| y2 |
| b2 |
因为双曲线的离心率为
| 5 |
| 1+b2 |
| 5 |
所以双曲线C的方程为x2-
| y2 |
| 4 |
(2)证明:设点P(x1,y1)、T(x2,y2)(xi>0,yi>0,i=1,2),直线AP的斜率为k(k>0),
则直线AP的方程为y=k(x+1),…(4分)
代入椭圆方程整理,得(4+k2)x2+2k2x+k2-4=0,
解得x=-1或x=
| 4-k2 |
| 4+k2 |
所以x2=
| 4-k2 |
| 4+k2 |
同理可得,x1=
| 4+k2 |
| 4-k2 |
所以x1•x2=1.…(8分)
点评:本小题主要考查椭圆与双曲线的方程、直线与圆锥曲线的位置关系等知识,考查化归与转化的数学思想方法,以及推理论证能力和运算求解能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
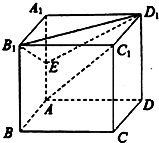 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中, 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.