题目内容
△ABC中,内角A、B、C所对边分别为a、b、c,己知A=
,c=
,b=1,
(1)求a的长及B的大小:
(2)若0<x<B,求函数f(x)=2sinxcosx+2
cos2x-
的值域.
| π |
| 6 |
| 3 |
(1)求a的长及B的大小:
(2)若0<x<B,求函数f(x)=2sinxcosx+2
| 2 |
| 3 |
考点:余弦定理,两角和与差的正弦函数
专题:三角函数的求值
分析:(1)利用余弦定理列出关系式,将b,c及cosA的值代入求出a的值,得到a=b,利用等边对等角得到A=B,即可求出B的度数;
(2)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化简,根据x的范围求出这个角的范围,利用正弦函数的值域即可确定出f(x)的值域.
(2)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化简,根据x的范围求出这个角的范围,利用正弦函数的值域即可确定出f(x)的值域.
解答:
解:(1)∵△ABC中,A=
,c=
,b=1,
∴由余弦定理得:a2=b2+c2-2bccosA=1+3-2
×
=1,即a=1,
∴a=b=1,
∴B=A=
;
(2)f(x)=2sinxcosx+2
cos2x-
=sin2x+
cos2x=2sin(2x+
),
∵0<x<
,得到
<2x+
<
,
∴
<sin(2x+
)≤1,即
<2sin(2x+
)≤2,
则函数的值域为(
,2].
| π |
| 6 |
| 3 |
∴由余弦定理得:a2=b2+c2-2bccosA=1+3-2
| 3 |
| ||
| 2 |
∴a=b=1,
∴B=A=
| π |
| 6 |
(2)f(x)=2sinxcosx+2
| 2 |
| 3 |
| 3 |
| π |
| 3 |
∵0<x<
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| ||
| 2 |
| π |
| 3 |
| 3 |
| π |
| 3 |
则函数的值域为(
| 3 |
点评:此题考查了余弦定理,二倍角的正弦、余弦函数公式,以及正弦函数的值域,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
从6名教师中选4名开设A,B,C,D四门课程,每人开设一门课程且开设的课程各不相同,若这6名教师中甲、乙两人不开设A课程,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
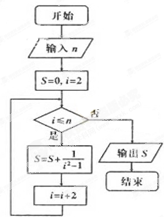
如图所示的程序框图,则输出的结果为( )


| A、189 | B、381 |
| C、93 | D、45 |
已知实数x、y满足约束条件
,若向量
=(x,y),向量
=(3,-1).设z表示向量
在向量
方向上的投影,则z的最大值是( )
|
| a |
| b |
| a |
| b |
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、6 |