题目内容
8.在下列A、B、C、D四个图象中,大致为函数y=2|x|-x2(x∈R)的图象的是( )| A. |  | B. | 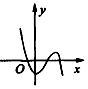 | C. | 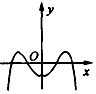 | D. | 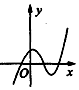 |
分析 分析函数的奇偶性,可排除B,D;由函数图象过(0,1)点,可排除C;进而得到答案.
解答 解:函数y=f(x)=2|x|-x2满足f(-x)=f(x),
即函数为偶函数,图象关于y轴对称,
故排除B,D;
当x=0时,函数图象过(0,1)点,
故排除C;
故选:A
点评 本题考查的知识点是函数的图象,对于超越函数图象的判断,多采用排除法进行解答.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16.已知全集U=R,集合A={x|x2-2x≤0},B={x|y=lg(x-1)},则集合A∩(∁UB)=( )
| A. | {x|x<0,或x>2} | B. | {x|0<x<2} | C. | {x|0≤x<1} | D. | {x|0≤x≤1} |
17.如图所示,在△ABC中,M在BC上,N在AM上,CM=CN,且$\frac{AM}{AN}$=$\frac{BM}{CN}$,下列结论中正确的是( )
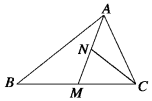

| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |
 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.