题目内容
两台车床加工同一种机械零件如下表:
从这100个零件中任取一个零件,求:
(1)取得合格品的概率;
(2)取得零件是第一台车床加工的合格品的概率.
| 合格品 | 次品 | 总计 | |
| 第一台车床加工的零件数 | 35 | 5 | 40 |
| 第二台车床加工的零件数 | 50 | 10 | 60 |
| 总计 | 85 | 15 | 100 |
(1)取得合格品的概率;
(2)取得零件是第一台车床加工的合格品的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据概率公式计算即可,
(2)先求出是第一台加工的概率,再求出第一台加工的合格品的概率,问题得以解决.
(2)先求出是第一台加工的概率,再求出第一台加工的合格品的概率,问题得以解决.
解答:
解:(1)这100个零件中,合格的有85,不合格的15,故从这100个零件中任取一个零件取得合格品的概率P=
=0.85;
(2)这100个零件中,第一台加工的有40个,第二台加工的有60,从这100个零件中任取一个零件是第一台加工的概率为
=
,第一台车床加工的合格品的概率为
=
,
所以取得零件是第一台车床加工的合格品的概率P=
×
=
.
| 85 |
| 100 |
(2)这100个零件中,第一台加工的有40个,第二台加工的有60,从这100个零件中任取一个零件是第一台加工的概率为
| 40 |
| 100 |
| 2 |
| 5 |
| 35 |
| 40 |
| 7 |
| 8 |
所以取得零件是第一台车床加工的合格品的概率P=
| 2 |
| 5 |
| 7 |
| 8 |
| 7 |
| 20 |
点评:本题主要考查了古典概率的问题,关键是找到基本事件.

练习册系列答案
相关题目
| ∫ | 2 -2 |
| A、0 | B、1 | C、8 | D、16 |
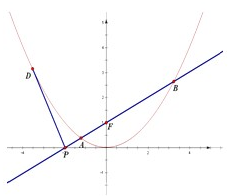 抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.
抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.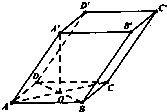 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=