题目内容
18.如图1,在直角梯形ABCD中,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}CD$=1,如图2,将△ABD沿BD折起来,使平面ABD⊥平面BCD,设E为AD的中点,F为AC上一点,O为BD的中点.(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)若AF=2FC,求三棱锥A-BEF的体积.
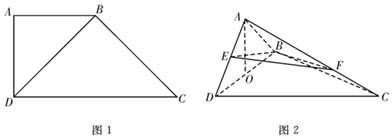
分析 (I)利用面面垂直的性质即可得出AO⊥平面BCD;
(II)证明BC⊥平面ABD,于是F到平面ABD的距离d=$\frac{2}{3}$BC,故VA-BEF=VF-ABE=$\frac{1}{3}{S}_{△ABE}•d$.
解答 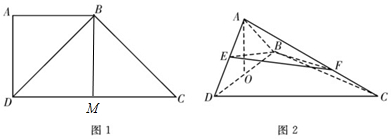 (I)证明:∵AB=AD,
(I)证明:∵AB=AD,
O是BD的中点,
∴AO⊥BD,
又∵平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
AO?平面ABD,
∴AO⊥平面BCD.
(II)解:在图1中,过B作BM⊥CD,垂足为M,则BM=AD=DM=CM=1,
∴∠DBM=∠CBM=45°,
∴BD⊥BC,BC=$\sqrt{2}$,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC?平面BCD,
∴BC⊥平面ABD,
∵AF=2FC,∴F到平面ABD的距离d=$\frac{2}{3}$BC=$\frac{2\sqrt{2}}{3}$,
∴VA-BEF=VF-ABE=$\frac{1}{3}{S}_{△ABE}•d$=$\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{18}$.
点评 本题考查了面面垂直的性质,线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
9.已知P:?x>0,lnx<x,则¬P为( )
| A. | ?x≤0,lnx0>x0 | B. | ?x≤0,lnx0≥x0 | C. | ?x>0,lnx0≥x0 | D. | ?x>0,lnx0<x0 |
13.“a>0”是“$a+\frac{2}{a}≥2\sqrt{2}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的( )
| A. | 否命题 | B. | 逆命题 | C. | 逆否命题 | D. | 否定形式 |
7.已知全集U=R,A={x|x2-2x<0},B={x|x≥1},则A∪(∁UB)=( )
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,2) | D. | (0,1) |
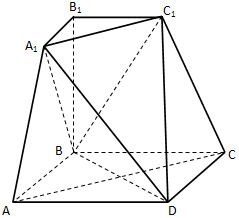 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.