题目内容
12.双曲线mx2+y2=1(m∈R)的离心率为$\sqrt{2}$,则m的值为( )| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
分析 化双曲线方程为标准方程,求出a,b,c,运用离心率公式可得m的方程,解方程即可得到.
解答 解:双曲线mx2+y2=1(m<0),
化为y2-$\frac{{x}^{2}}{-\frac{1}{m}}$=1,
即有a=1,b=$\sqrt{-\frac{1}{m}}$,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{1-\frac{1}{m}}$,
由题意可得e=$\frac{c}{a}$=$\sqrt{1-\frac{1}{m}}$=$\sqrt{2}$,
解得m=-1,
故选:B.
点评 本题考查双曲线的方程和性质,注意运用双曲线的基本量a,b,c和离心率公式,考查方程思想和运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.四个数40.2,30.5,30.4,log0.40.5的大小顺序是( )
| A. | ${4^{0.2}}<{3^{0.4}}<{log_{0.4}}0.5<{3^{0.5}}$ | B. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}<{3^{0.5}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.5}}<{4^{0.2}}<{3^{0.4}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}<{3^{0.5}}$ |
3.已知偶函数f(x)的定义域为R,且在(-∞,0)上是增函数,则f(-$\frac{3}{4}$)与f(a2-a+1)的大小关系为( )
| A. | f(-$\frac{3}{4}$)<f(a2-a+1) | B. | f(-$\frac{3}{4}$)>f(a2-a+1) | C. | f(-$\frac{3}{4}$)≤f(a2-a+1) | D. | f(-$\frac{3}{4}$)≥f(a2-a+1) |
20.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)四边形;(3)五边形;(4)六边形,其中正确的结论是( )
| A. | (1)(3) | B. | (2)(4) | C. | (2)(3)(4) | D. | (1)(2)(3)(4) |
17.已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R满足f(x)+f′(x)<0,则下列结论正确的是( )
| A. | e2f(2)>e3f(3) | B. | e2f(2)<e3f(3) | C. | e2f(2)≥e3f(3) | D. | e2f(2)≤e3f(3) |
2.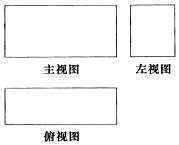 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )| A. | 3$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 6$\sqrt{5}$+4 | D. | 10 |
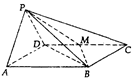 如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.
如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.