题目内容
7.已知双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$的左右焦点分别为F1,F2,O为坐标原点,P为双曲线右支上一点,△F1PF2的内切圆的圆心为Q,过F2作PQ的垂线,垂足为B,则OB的长度为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
分析 利用垂直平分线的性质,结合双曲线的定义,把|PF1|-|PF2|=2a,转化为|PF1|-|PC|=2a,在△F1CF2中,利用中位线定理得出OB,从而得到结论.
解答 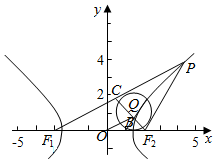 解:根据题意得F1(-c,0),F2(c,0),
解:根据题意得F1(-c,0),F2(c,0),
由△PF1F2的内切圆的圆心为Q,
点P在双曲线右支上,
可得|PF1|-|PF2|=2a,
在△F1CF2中,
OB=$\frac{1}{2}$CF1=$\frac{1}{2}$(PF1-PC)
=$\frac{1}{2}$(PF1-PF2)=$\frac{1}{2}$•2a=a,
则|OB|的长度为a=2.
故选:D.
点评 本题考查OB线段长的求法,是中档题,解题时要熟练掌握双曲线简单性质的灵活运用,以及内切圆的性质,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
15.集合A={x∈N|-1<x<4}的真子集个数为( )
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
18.已知双曲线的$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$的一条渐近线为2x+y=0,则该双曲线的离心率等于( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
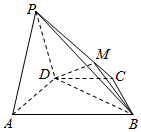 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.