题目内容
19．已知函数f（x）=4x2-6x+2．（1）求f（x）的单调区间
（2）f（x）在[2，4]上的最大值．
分析 （1）（2）配方利用二次函数的单调性即可得出．
解答 解：（1）函数f（x）=4x2-6x+2=4$（x-\frac{3}{4}）^{2}$-$\frac{1}{4}$，
∴函数f（x）在区间$（-∞，\frac{3}{4}）$上单调递减，在区间$[\frac{3}{4}，+∞）$上单调递增．
（2）由（1）可知：f（x）在[2，4]上单调递增，
∴当x=4时，函数f（x）取得最大值，f（4）=4×42-6×4+2=42．
点评 本题考查了二次函数的单调性、配方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
9．设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x，且一个焦点与抛物线x2=4y的焦点相同，则此双曲线的方程为（ ）
| A． | $\frac{5}{4}$x2-5y2=1 | B． | 5y2-$\frac{5}{4}$x2=1 | C． | $\frac{5}{4}$y2-5x2=1 | D． | 5x2-$\frac{5}{4}$y2=1 |
7．已知双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$的左右焦点分别为F1，F2，O为坐标原点，P为双曲线右支上一点，△F1PF2的内切圆的圆心为Q，过F2作PQ的垂线，垂足为B，则OB的长度为（ ）
| A． | $\sqrt{7}$ | B． | 4 | C． | 3 | D． | 2 |
14．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a，b＞0）的右焦点F，且斜率为2的直线l与双曲线的相交于点A，B，若弦AB的中点横坐标取值范围为（2c，4c），则该双曲线的离心率的取值范围是（ ）
| A． | （3，4） | B． | （2，3） | C． | $（\sqrt{3}，4）$ | D． | $（\sqrt{3}，2）$ |
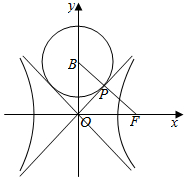如图，双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a，b＞0）虚轴上的端点B（0，b），右焦点F，若以B为圆心的圆与C的一条渐近线相切于点P，且$\overrightarrow{BP}$∥$\overrightarrow{PF}$，则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$．
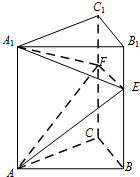如图，正三棱柱ABC-A1B1C1中，AB=4，AA1=6．若E，F分别是棱BB1，CC1上的点，则三棱锥A-A1EF的体积是8$\sqrt{3}$．
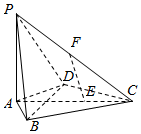在四棱锥P-ABCD中，PA⊥底面ABCD，AB=AD=2，CB=CD=$\sqrt{7}$，∠BAD=120°，点E在线段AC上，且AE=2EC，F为线段PC的中点．