题目内容
17.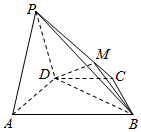 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.(Ⅰ)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(Ⅱ)求四棱锥P-ABCD的体积.
分析 (I)欲证平面MBD⊥平面PAD,根据面面垂直的判定定理可知在平面MBD内一直线与平面PAD垂直,而根据平面PAD与平面ABCD垂直的性质定理可知BD⊥平面PAD;
(II)过P作PO⊥AD交AD于O,根据平面PAD与平面ABCD垂直的性质定理可知PO⊥平面ABCD,从而PO为四棱锥P-ABCD的高,四边形ABCD是梯形,根据梯形的面积公式求出底面积,最后用锥体的体积公式进行求解即可.
解答  (Ⅰ)证明:在△ABD中,由于AD=2,BD=4,$AB=2\sqrt{5}$,
(Ⅰ)证明:在△ABD中,由于AD=2,BD=4,$AB=2\sqrt{5}$,
∴AD2+BD2=AB2.故AD⊥BD.…(2分)
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面PAD.…(4分)
又BD?平面MBD,故平面MBD⊥平面PAD.…(6分)
(Ⅱ)解:过P作PO⊥AD交AD于O,由于平面PAD⊥平面ABCD,
∴PO⊥平面ABCD.∴PO为四棱锥P-ABCD的高.…(7分)
又△PAD是边长为2的等边三角形,
∴$PO=\frac{{\sqrt{3}}}{2}×2=\sqrt{3}$.…(8分)
在底面四边形ABCD中,AB∥DC,AB=2DC,所以四边形ABCD是梯形.…(9分)
在Rt△ADB中,斜边AB边上的高为$\frac{2×4}{{2\sqrt{5}}}=\frac{{4\sqrt{5}}}{5}$,…(10分)
∴四边形ABCD的面积为$S=\frac{{2\sqrt{5}+\sqrt{5}}}{2}×\frac{{4\sqrt{5}}}{5}=6$.…(11分)
故${V_{P-ABCD}}=\frac{1}{3}×6×\sqrt{3}=2\sqrt{3}$.…(12分)
点评 本小题主要考查平面与平面垂直的判定,以及棱锥的体积等有关知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于中档题.

| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
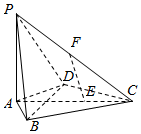 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.