题目内容
18.已知双曲线的$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$的一条渐近线为2x+y=0,则该双曲线的离心率等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
分析 求得双曲线的渐近线方程,由题意可得a=2b,运用a,b,c的关系和离心率公式,计算即可得到所求值.
解答 解:双曲线$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$的渐近线方程为y=±$\frac{a}{b}$x,
由一条渐近线为2x+y=0,可得$\frac{a}{b}$=2,
即a=2b,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{5}}{2}$a,
可得e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程,考查运算能力,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
9.设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x,且一个焦点与抛物线x2=4y的焦点相同,则此双曲线的方程为( )
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |
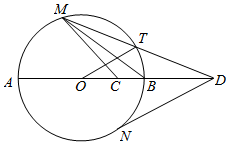 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT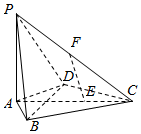 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.