题目内容
在△ABC中,A>B>C,B=60°,sinA-sinC+
cos(A-C)=
,
(1)求A,C大小;
(2)当x∈[0,
]时,求函数y=sin(2x+A)的最值.
| ||
| 2 |
| ||
| 2 |
(1)求A,C大小;
(2)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(1)利用和差化积公式与二倍角的余弦可求得sin
=
,从而可求A,C大小;
(2)x∈[0,
],A=105°=
⇒2x+A=2x+
∈[
,
]⇒-1≤sin(2x+
)≤sin
=
,从而可求得函数y=sin(2x+A)的最值.
| A-C |
| 2 |
| ||
| 2 |
(2)x∈[0,
| π |
| 2 |
| 7π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
| 19π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
| ||||
| 4 |
解答:
解:(1)∵△ABC中,A>B>C,B=60°,
∴A+C=120°,①
又sinA-sinC+
cos(A-C)=
,
∴2cos
•sin
+
(1-2sin2
)=
,
即sin
+
-
sin2
=
,
∴sin
(1-
sin
)=0,sin
≠0,
∴sin
=
,0°<
<60°,
∴
=45°,②
由①②得A=105°,C=15°.
(2)∵x∈[0,
],A=105°=
,
∴2x+A=2x+
∈[
,
],
∴-1≤sin(2x+
)≤sin
,
又sin
=sin(
+
)=sin
cos
+cos
sin
=
×
+
×
=
,
∴y=sin(2x+A)∈[-1,
],
∴y=sin(2x+A)的最小值为-1,最大值
.
∴A+C=120°,①
又sinA-sinC+
| ||
| 2 |
| ||
| 2 |
∴2cos
| A+C |
| 2 |
| A-C |
| 2 |
| ||
| 2 |
| A-C |
| 2 |
| ||
| 2 |
即sin
| A-C |
| 2 |
| ||
| 2 |
| 2 |
| A-C |
| 2 |
| ||
| 2 |
∴sin
| A-C |
| 2 |
| 2 |
| A-C |
| 2 |
| A-C |
| 2 |
∴sin
| A-C |
| 2 |
| ||
| 2 |
| A-C |
| 2 |
∴
| A-C |
| 2 |
由①②得A=105°,C=15°.
(2)∵x∈[0,
| π |
| 2 |
| 7π |
| 12 |
∴2x+A=2x+
| 7π |
| 12 |
| 7π |
| 12 |
| 19π |
| 12 |
∴-1≤sin(2x+
| 7π |
| 12 |
| 7π |
| 12 |
又sin
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
∴y=sin(2x+A)∈[-1,
| ||||
| 4 |
∴y=sin(2x+A)的最小值为-1,最大值
| ||||
| 4 |
点评:本题考查三角函数中的恒等变换,考查和差化积公式与二倍角的余弦,突出正弦函数单调性与两角和的正弦的考查,属于难题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
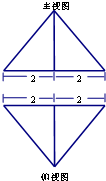 三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )
三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )