在平面直角坐标系xoy中.曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.$.直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$以坐标原� 题目和参考答案——青夏教育精英家教网——

题目内容

15．在平面直角坐标系xoy中，曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.$（θ为参数），直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数）以坐标原点O为极点，x轴的正半轴为极轴的极坐标系．
（1）写出直线l的普通方程以及曲线C的极坐标方程；
（2）若直线l与曲线C的两个交点分别为M，N，直线l与x轴的交点为P，求|PM|•|PN|的值．

分析（1）直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），消去参数t可得普通方程．曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.$（θ为参数），利用平方关系可得直角坐标方程．把ρ²=x²+y²，y=ρsinθ，可得C的极坐标方程．
（II）P（1，0）．把直线l的参数方程代入圆C的方程为：${t}^{2}-3\sqrt{2}t$+1=0，|PM|•|PN|=|t₁•t₂|．

解答解：（1）直线l的参数方程为$\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），消去参数t可得：x+y-1=0．
曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.$（θ为参数），利用平方关系可得：x²+（y-2）²=4．
把ρ²=x²+y²，y=ρsinθ，可得C的极坐标方程为：ρ=4sinθ．
（II）P（1，0）．把直线l的参数方程代入圆C的方程为：${t}^{2}-3\sqrt{2}t$+1=0，
t₁+t₂=3$\sqrt{2}$，t₁•t₂=1，
∴|PM|•|PN|=|t₁•t₂|=1．

点评本题考查了极坐标方程的应用、参数方程化为普通方程、直线与圆相交弦长问题，考查了推理能力与计算能力，属于中档题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

5．已知函数f（x）=alnx-$\frac{1}{2}{x^2}$+bx存在极小值，则有（　　）

6．已知变量x，y满足约束条件$\left\{\begin{array}{l}x-y≥2\\ x+y≤4\\ y≥-1\end{array}\right.$，则目标函数z=x-2y的最小值为（　　）

某地政府拟在该地一水库上建造一座水电站，用泄流水量发电．图是根据该水库历年的日泄流量的水文资料画成的日泄流量X（单位：万立方米）的频率分布直方图（不完整），已知X∈[0，120），历年中日泄流量在区间[30，60）的年平均天数为156，一年按364天计．
（Ⅰ）请把频率分布直方图补充完整；
（Ⅱ）已知一台小型发电机，需30万立方米以上的日泄流量才能运行，运行一天可获利润为4000元，若不运行，则每天亏损500元；一台中型发电机，需60万立方米以上的日泄流量才能运行，运行一天可获利10000元，若不运行，则每天亏损800元；根据历年日泄流量的水文资料，水电站决定安装一台发电机，为使一年的日均利润值最大，应安装哪种发电机？

10．在平面直角坐标系xOy中，过点M（0，1）的椭圆 Γ：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$
（1）求椭圆 Γ的方程；
（2）已知直线l不过点M，与椭圆 Γ相交于P，Q两点，若△MPQ的外接圆是以PQ为直径，求证：直线l过定点，并求出该定点的坐标．

20．已知函数$f（x）=\frac{f'（1）}{e}{e^x}+\frac{f（0）}{2}{x^2}-x$，若存在实数m使得不等式f（m）≤2n²-n成立，求实数n的取值范围为（　　）

$（{-∞，-\frac{1}{2}}]∪[{1，+∞}）$

$（{-∞，-1}]∪[{\frac{1}{2}，+∞}）$

$（{-∞，0}]∪[{\frac{1}{2}，+∞}）$

$（{-∞，-\frac{1}{2}}]∪[{0，+∞}）$

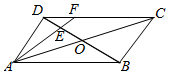在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F．若AB=2，$AD=\sqrt{2}$，∠BAD=45°，则$\overrightarrow{AF}•\overrightarrow{BE}$=（　　）

4．已知数列{a_n}是单调递减的等差数列，S₆=S₁₁，有以下四个结论：
（1）a₉=0
（2）当n=8或n=9时，S_n取最大值
（3）存在正整数k使得S_k=0
（4）存在正整数m使得S_m=S_2m
其中正确的是（1），（2），（3）．

5．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递减，若实数a满足f（log₃a）+f（${log}_{\frac{1}{3}}$a）≤2f（2），则a的取值范围是（　　）

[$\frac{1}{9}$，9]

（-∞，$\frac{1}{9}$]

[$\frac{1}{2}$，2]

（0，$\frac{1}{9}$]∪[9，+∞]