题目内容
17.某厂用甲、乙两种原料生产A、B两种产品,已知生产1吨A产品,1吨B产品分别需要的甲、乙原料数,每种产品可获得的利润数及该厂现有原料数如表所示.| 产品 所需原料 原料 | A产品 (1吨) | B产品 (1吨) | 现有原料 (吨) |
| 甲原料(吨) | 4 | 5 | 200 |
| 乙原料(吨) | 3 | 10 | 300 |
| 利润(万元) | 7 | 12 |
分析 生产A、B产品分别为x,y吨,利润总额为z元,列出约束条件,作出可行域,根据可行域寻找最优解.
解答 解:设生产A、B产品分别为x,y吨,利润总额为z元,
由题意得$\left\{\begin{array}{l}{4x+5y≤200}\\{3x+10y≤300}\\{x≥0}\\{y≥0}\end{array}\right.$.
目标函数为z=7x+12y.
作出二元一次不等式组所表示的可行域,如图: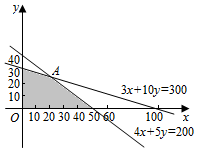
目标函数可变形为$y=-\frac{7}{12}x+\frac{1}{12}z$,
∵-$\frac{4}{5}$<-$\frac{7}{12}$<-$\frac{3}{10}$,
∴当$y=-\frac{7}{12}x+\frac{1}{12}z$通过图中的点A时,截距$\frac{1}{12}z$最大,即z最大.
解$\left\{\begin{array}{l}{4x+5y=200}\\{3x+10y=300}\end{array}\right.$得点A坐标为(20,24).
将点A(20,24)代入z=7x+12y
得zmax=7×20+12×24=428万元.
答:该厂生产A,B两种产品分别为20吨、24吨时利润最大,最大利润为428万元.
点评 本题考查了简单的线性规划应用,根据题意列出约束条件作出可行域是解题关键.

练习册系列答案
相关题目
2.设10件产品中含有3件次品,从中抽取2件进行检查,则查得的次品数的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{15}$ | D. | $\frac{8}{15}$ |
5.设复数z满足z•i=2-i,i为虚数单位,
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
p1:|z|=$\sqrt{5}$,
p2:复数z在复平面内对应的点在第四象限;
p3:z的共轭复数为-1+2i,
p4:z的虚部为2i.
其中的真命题为( )
| A. | p1,p3 | B. | p2,p3 | C. | p1,p2 | D. | p1,p4 |
12.在△ABC中,若$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),则下列关系式正确的是( )
| A. | BD=2CD | B. | BD=CD | C. | BD=3CD | D. | CD=2BD |
2.已知关于x的方程${e^x}+{e^{-x}}-2a{log_2}(|x|+2)+{a^2}=5$有唯一实数解,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或-3 |
7.已知函数f(x)=$\left\{\begin{array}{l}{x^4}+1,x>0\\ cos2x,x≤0\end{array}\right.$,则下列结论正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是增函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,+∞) |