题目内容

设f（x）是定义域为R的奇函数，且当x＞0时，f（x）=x2-x，则f（-2）=（　　）
A、2B、-2C、6D、-6
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由f（x）是定义域为R的奇函数得f（-2）=-f（2）=-（4-2）=-2．
解答： 解：∵f（x）是定义域为R的奇函数，
∴f（-2）=-f（2）=-（4-2）=-2；
故选B．
点评：本题考查了函数性质的应用，属于基础题．
练习册系列答案
相关题目
已知向量
a
=（sin2x，cos2x），
b
=（
1
2
，
3
2
），x∈R，且f（x）=
a
•
b
+|
a
|+|
b
|．
（1）求函数f（x）的单调递增区间；
（2）若x∈[
π
6
，
2π
3
]，求函数f（x）的最大值和最小值．
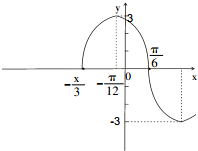已知函数f（x）=Asin（ωx+φ）（A＞0，ω，0，|φ|＜π）的部分图象如图所示．
（1）求函数f（x）解析式；
（2）说明y=f（x）的图象如何由y=sinx的图象变换得到的（填空）
y=sinx（
 
）→（　y=sin（x+
2π
3
）　）
（
 
）→（y=sin（2x+
2π
3
））
（
 
）→（f（x）=3sin（2x+
2π
3
））
给出定义：若m-
1
2
＜x≤m+
1
2
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m．在此基础上给出下列关于函数f（x）=x-{x}的四个判断：
①y=f（x）的定义域是R，值域是（-
1
2
，
1
2
]；
②点（k，0）是y=f（x）的图象的对称中心，其中k∈Z；
③函数y=f（x）的最小正周期为1；
④函数y=f（x）在（
1
2
，
3
2
]上是增函数．
则上述判断中正确的序号是
 
．（填上所有正确的序号）
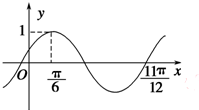函数f（x）=Asin（ωx+φ） （A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）将y=f（x）的图象向右平移
π
6
个单位后得到新函数g（x）的图象，求函数g（x）的解析式；
（Ⅲ）求函数2f（x）-g（x）的单调增区间．
画出g（x）=x2-4|x|的图象，并解x2-4|x|＜-3．
已知a＞0，b＞0，a+3b=ab+1，求a+3b的范围．
已知α∈（π，2π），cosα=
3
5
，则tan(α+
π
4
)等于
 
．
若cosa=-
4
5
，且a是第三象限角，则tana=（　　）
A、-
3
4
B、
3
4
C、
4
3
D、-
4
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网