题目内容
已知y=f(x)=ln|x|,则下列各命题中,正确的命题是( )
A.x>0时,f′(x)= ,x<0时,f′(x)=﹣
,x<0时,f′(x)=﹣
B.x>0时,f′(x)= ,x<0时,f′(x)无意义
,x<0时,f′(x)无意义
C.x≠0时,都有f′(x)=
D.∵x=0时f(x)无意义,∴对y=ln|x|不能求导
C
【解析】
试题分析:利用绝对值的意义将函数中的绝对值去掉转换为分段函数;利用基本的初等函数的导数公式及复合函数的求导法则:外函数的导数与内函数的导数的乘积,分别对两段求导数,两段的导数合起来是f(x)的导数.
【解析】
根据题意,f(x)= ,
,
分两种情况讨论:
(1)x>0时,f(x)=lnx⇒f'(x)=(lnx)'= .
.
(2)x<0时f(x)=ln(﹣x)⇒f'(x)=[ln(﹣x)]'= (这里应用定义求导.)
(这里应用定义求导.)
故选C

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的前
的前 项和记为
项和记为 ,已知
,已知 ,求
,求 ______________.
______________.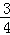 ,次品率为
,次品率为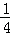 ,现对该批电子手表进行测试,设第X次首次测到正品,则P(1≤X≤2013)等于( )
,现对该批电子手表进行测试,设第X次首次测到正品,则P(1≤X≤2013)等于( )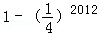
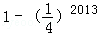
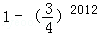
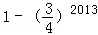
 .
.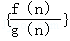 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( ) 等于( )
等于( )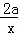 +3a,若f′(﹣1)=8,则f(﹣1)=( )
+3a,若f′(﹣1)=8,则f(﹣1)=( )