题目内容
(本小题满分14分)设函数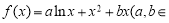 R
R ,且
,且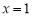 为
为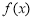 的极值点.
的极值点.
(1)当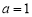 时,求
时,求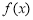 的单调递减区间;
的单调递减区间;
(2)若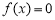 恰有两解,试求实数
恰有两解,试求实数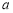 的取值范围;
的取值范围;
(3)在(1)的条件下,设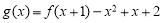 ,证明:
,证明: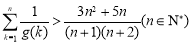 .
.
(1)单调减区间为 ;(2)
;(2)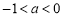 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:由已知求导得:  ,由
,由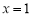 为
为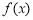 的极值点,
的极值点,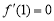 ,
, 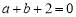 .
.
(1)当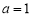 时,
时,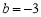 ,进而
,进而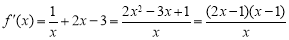 ,又函数
,又函数 的定义域为
的定义域为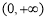 ,即可求出函数的单调见区间.(2)由
,即可求出函数的单调见区间.(2)由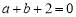 ,得
,得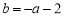 ,则
,则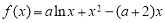 ,
,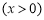 ,
, 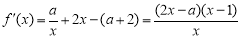 ,
,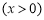 ,对a进行分类讨论即可求出结果;(3)当
,对a进行分类讨论即可求出结果;(3)当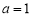 时,
时,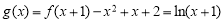 ,即证:
,即证: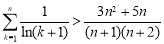 .(方法一)利用不等式放缩即可求出结果;(方法二)数学归纳法,证明即可.
.(方法一)利用不等式放缩即可求出结果;(方法二)数学归纳法,证明即可.
试题解析:【解析】
由已知求导得:  ,
,
 为
为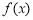 的极值点,
的极值点,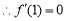 ,
, 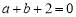 . 2分
. 2分
(1)当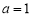 时,
时,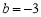 ,
,
进而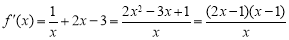 ,
,
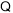 函数
函数 的定义域为
的定义域为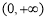 ,
,
 的单调减区间为
的单调减区间为 . 4分
. 4分
(2)由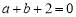 ,得
,得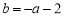 ,则
,则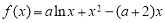 ,
,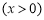 ,
,
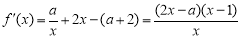 ,
,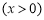 ,
,
(ⅰ)当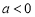 时,
时,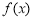 在
在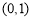 递减,在
递减,在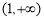 递增,则
递增,则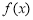 的极小值为
的极小值为 ,
,
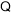
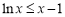 ,
,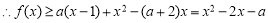 ,
,
则当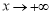 时,
时,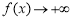 ,
,
又 当
当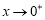 时,
时,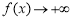 ,
, 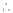 要使
要使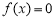 恰有两解,须
恰有两解,须 ,即
,即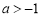 .
.
因此,当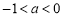 时,
时,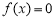 恰有两解.
恰有两解.
(ⅱ)当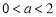 时,
时,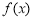 在
在 、
、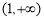 递增,在
递增,在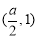 递减,
递减,
则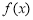 的极大值为
的极大值为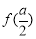 ,
, 的极小值为
的极小值为 .
.
 ,
,
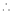 当
当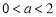 时,
时,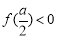 ,此时
,此时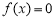 不可能恰有两解.
不可能恰有两解.
(ⅲ)当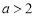 时,
时, 在
在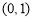 、
、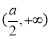 递增,在
递增,在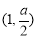 递减,
递减,
则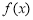 的极大值为
的极大值为 ,
, 的极小值为
的极小值为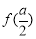 .
.
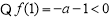 ,
, 当
当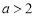 时,
时,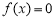 不可能恰有两解.
不可能恰有两解.
(ⅳ)当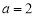 时,
时,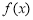 在
在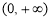 单调递增,
单调递增,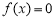 不可能恰有两解.
不可能恰有两解.
综合可得,若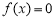 恰有两解,则实数
恰有两解,则实数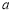 的取值范围是
的取值范围是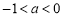 . 9分
. 9分
(3)当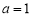 时,
时,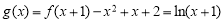 ,
,
即证: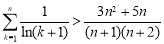 .
.
(方法一)先证明:当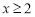 时,
时,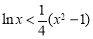 .
.
设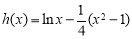 ,
,  ,
,
当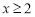 时,
时,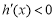 ,则
,则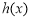 在
在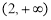 递减,
递减,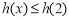 ,
,
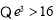 ,
,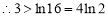 ,即
,即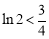 ,
,
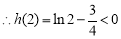 ,
,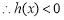 ,即
,即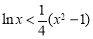 .
.
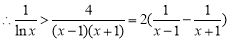 .
.
令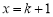 ,得
,得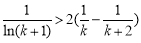 ,
,
则 . 14分
. 14分
(方法二)数学归纳法:
1.当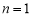 时,左边=
时,左边=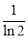 ,右边=
,右边=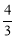 ,
,
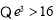 ,
,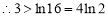 ,
, 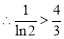 ,即
,即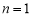 时,命题成立.
时,命题成立.
2.设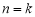 时,命题成立,即
时,命题成立,即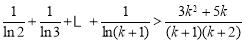 .
.
当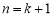 时,左边=
时,左边=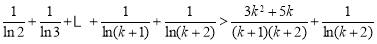
右边=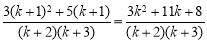 ,
,
要证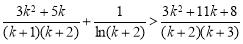 ,即证
,即证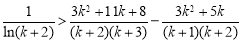 ,
,
即证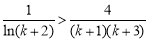 ,也即证
,也即证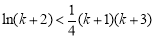 .
.
令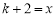 ,即证:
,即证: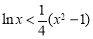 ,(证法见方法一)
,(证法见方法一)
因此,由数学归纳法可得命题成立. 14分.
考点:1.导数在函数单调区间上的应用;2.导数在证明不等式中的应用.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 的虚部是( )
的虚部是( ) B.
B. C.
C. D.
D.
 sin2x+
sin2x+ cos2x,若将函数f(x)的图象向右平移
cos2x,若将函数f(x)的图象向右平移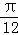 个单位,所得图象对应函数为g(x),则( )
个单位,所得图象对应函数为g(x),则( )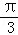 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称 ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称 ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 满足
满足 ,则不等式组所表示的平面区域的面积为_________.
,则不等式组所表示的平面区域的面积为_________.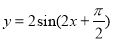 是( )
是( ) 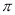 的奇函数 B.周期为
的奇函数 B.周期为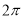 的奇函数 D.周期为
的奇函数 D.周期为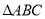 中,设角
中,设角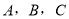 的对边分别为
的对边分别为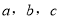 ,且
,且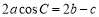 .
.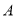 的大小;
的大小;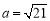 ,
,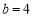 ,求边
,求边 的大小.
的大小.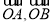 不共线,向量
不共线,向量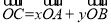 ,则下列命题正确的是
,则下列命题正确的是 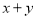 为定值,则
为定值,则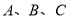 三点共线.
三点共线. 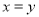 ,则点
,则点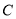 在
在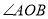 的平分线所在直线上.
的平分线所在直线上. 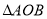 的重心,则
的重心,则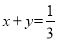 .
.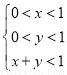 .
. 在
在 不是单调函数,则
不是单调函数,则 的范围是 .
的范围是 . (
( ,
, ),若数列
),若数列 是等差数列,记集合
是等差数列,记集合 的元素个数为
的元素个数为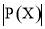 ,则
,则 关于
关于 的表达式为 .
的表达式为 .