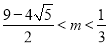题目内容
(本小题满分12分)在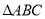 中,设角
中,设角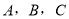 的对边分别为
的对边分别为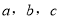 ,且
,且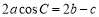 .
.
(1)求角 的大小;
的大小;
(2)若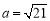 ,
,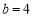 ,求边
,求边 的大小.
的大小.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)解三角形问题,一般利用正弦定理或余弦定理将边统一为角或将角统一为边,如用正弦定理将 化为角
化为角 也可用余弦定理将
也可用余弦定理将 化为边
化为边 ,在统一为角后,再利用诱导公式将三个角化为两个角,结合两角和与差公式将两个角化为所求角;在统一为边后,再利用余弦定理或勾股定理求对应角,(2)结合(1)知,所求问题为已知一角两边,求第三边,显然用余弦定理比较直接.
,在统一为角后,再利用诱导公式将三个角化为两个角,结合两角和与差公式将两个角化为所求角;在统一为边后,再利用余弦定理或勾股定理求对应角,(2)结合(1)知,所求问题为已知一角两边,求第三边,显然用余弦定理比较直接.
试题解析:【解析】
(1)因为 ,所以
,所以


 4分
4分
即 ,
,
又因为 ,所以
,所以 ,
,
所以 ,
,
又因为
所以 . 8分
. 8分
(2) 因为 ,即
,即
所以 ,解得
,解得 (舍),
(舍), . 12分.
. 12分.
考点:1.解三角形;2.正弦定理;3.余弦定理.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
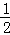 )上恒成立,求a的最小值.
)上恒成立,求a的最小值.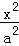 ﹣
﹣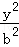 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为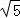 ,则C的渐近线方程为( )
,则C的渐近线方程为( )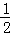 x C.y=±
x C.y=± x D.y=±
x D.y=±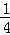 x
x 均为单位向量,且
均为单位向量,且 ,则
,则 与
与 夹角为( )
夹角为( )  B.
B. C.
C. D.
D.
 R
R ,且
,且 为
为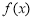 的极值点.
的极值点.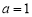 时,求
时,求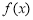 的单调递减区间;
的单调递减区间; 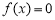 恰有两解,试求实数
恰有两解,试求实数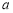 的取值范围;
的取值范围;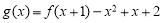 ,证明:
,证明: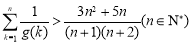 .
. 是定义在
是定义在 上的奇函数,则
上的奇函数,则 = .
= .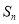 是等差数列
是等差数列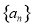 的前
的前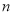 项和,已知
项和,已知 49,则
49,则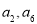 的等差中项是
的等差中项是 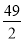 B.7 C.
B.7 C.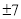 D.
D.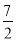
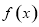 定义域
定义域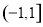 ,满足
,满足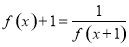 ,当
,当 时,
时,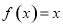 ,若函数
,若函数 ,方程
,方程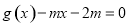 有三个实根,则实数
有三个实根,则实数 的取值范围是( )
的取值范围是( )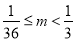 B.
B.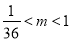 C.
C.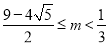 D.
D.