题目内容
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.(1)问点E在何处时,PA∥平面EBD,并加以证明;
(2)求二面角C-PA-B的余弦值.

【答案】分析:(1)由已知,只需证明PA与面EDB内一条直线平行即可,因此连接AC,EO,AC∩BD=O,则O为AC的中点,证出PA∥EO,则PA∥平面EBD
(2)取PA的中点F,连接OF,BF,证出∠BFO为二面角C-PA-B的平面角,解△BOF 即可.
解答:解:(1)当E为PC中点时,PA∥平面EBD
连接AC,EO,且AC∩BD=O
∵四边形ABCD为正方形,
∴O为AC的中点,又E为中点,
∴OE为△ACP的中位线,
∴PA∥EO
又PA?面EBD,EO?平面EBD
∴PA∥平面EBD
(2)取PA的中点F,连接OF,BF,
∵ ,∴CP⊥AP
,∴CP⊥AP
∵O,F为中点,
∴OF∥CP,即OF⊥PA,
又∵BP=BA,F为PA中点∴BF⊥PA,
所以∠BFO为二面角C-PA-B的平面角.
在正四棱锥P-ABCD中易得:
∴BF2=FO2+BO2,
∴△BOF为Rt△,
∴
点评:本题考查线面位置关系、二面角的度量,考查分析解决问题、空间想象、转化、计算的能力与方程思想.
(2)取PA的中点F,连接OF,BF,证出∠BFO为二面角C-PA-B的平面角,解△BOF 即可.
解答:解:(1)当E为PC中点时,PA∥平面EBD
连接AC,EO,且AC∩BD=O
∵四边形ABCD为正方形,
∴O为AC的中点,又E为中点,
∴OE为△ACP的中位线,
∴PA∥EO
又PA?面EBD,EO?平面EBD
∴PA∥平面EBD
(2)取PA的中点F,连接OF,BF,
∵
 ,∴CP⊥AP
,∴CP⊥AP∵O,F为中点,
∴OF∥CP,即OF⊥PA,
又∵BP=BA,F为PA中点∴BF⊥PA,
所以∠BFO为二面角C-PA-B的平面角.
在正四棱锥P-ABCD中易得:

∴BF2=FO2+BO2,
∴△BOF为Rt△,
∴

点评:本题考查线面位置关系、二面角的度量,考查分析解决问题、空间想象、转化、计算的能力与方程思想.

练习册系列答案
相关题目
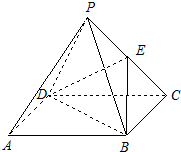 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.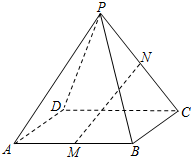 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点. 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )